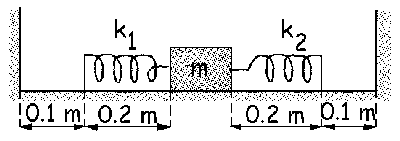
a) x1=0.35 m de la izquierda
b) k=k1+k2
c)T=0.99 s
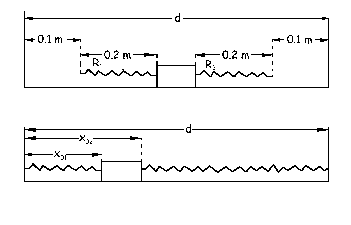 Tomaremos como eje X el horizontal y como eje Y el vertical. En la parte superior del gráfico adjunto se muestra la situación inicial. A continuación se unen los resortes a los postes y el bloque se desplaza hasta una cierta posición en la que quedaría en reposo y equilibrio, como aparece en la parte inferior de la figura. Llamaremos x01 a la distancia desde la parte derecha del bloque al poste, y x02 a la distancia desde la parte derecha del bloque al mismo poste. Ambos resortes estarán estirados para que el bloque tenga una posición de equilibrio, puesto que si uno de los resortes estuviera comprimido las fuerzas ejercidas por ambos resortes sobre el bloque tendrían el mismo sentido y no estaría en equilibrio
Tomaremos como eje X el horizontal y como eje Y el vertical. En la parte superior del gráfico adjunto se muestra la situación inicial. A continuación se unen los resortes a los postes y el bloque se desplaza hasta una cierta posición en la que quedaría en reposo y equilibrio, como aparece en la parte inferior de la figura. Llamaremos x01 a la distancia desde la parte derecha del bloque al poste, y x02 a la distancia desde la parte derecha del bloque al mismo poste. Ambos resortes estarán estirados para que el bloque tenga una posición de equilibrio, puesto que si uno de los resortes estuviera comprimido las fuerzas ejercidas por ambos resortes sobre el bloque tendrían el mismo sentido y no estaría en equilibrio
El resorte 1 estará estirado una cantidad x1 mientras que el resorte 2 estará estirado una cantidad x2.
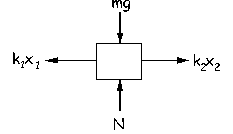 Trazamos el diagrama de sólido libre del bloque. Como el bloque está en equilibrio:
Trazamos el diagrama de sólido libre del bloque. Como el bloque está en equilibrio:
ΣFx=0 ⇒ k1x1-k2x2=0 ⇒ k1(x01-0.2)-k2(d-x02-0.2)=0
Además sabemos que:
d-(x02-x01)=0.1+0.2+0.2+0.1 ⇒ d-x02+x01=0.6
De esta última ecuación:
d-x02+x01=0.6 ⇒ d-x02=0.6-x01
Sustituyendo esta expresión en la ecuación de fuerzas:
k1(x01-0.2)-k2(d-x02-0.2)=0 ⇒ k1(x01-0.2)-k2(0.6-x01-0.2)=0 ⇒ 1(x01-0.2)-3(0.6-x01-0.2)=0
x01-0.2-1.8+3x01+0.6=0 ⇒ 4x01=1.4
De donde obtenemos:
x01=0.35 m
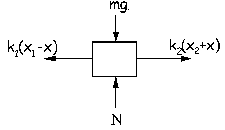 b) Supongamos ahora que desplazamos el bloque una cantidad x hacia la izquierda y lo dejamos oscilar. Tendremos el diagrama de fuerzas que aparece en la figura. El sistema ya no está en equilibrio. Tendremos que aplicando la segunda ley de Newton:
b) Supongamos ahora que desplazamos el bloque una cantidad x hacia la izquierda y lo dejamos oscilar. Tendremos el diagrama de fuerzas que aparece en la figura. El sistema ya no está en equilibrio. Tendremos que aplicando la segunda ley de Newton:
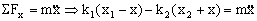
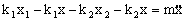
Por la condición de equilibrio sabemos que:
k1x1-k2x2=0
Por tanto eliminando estos términos de la ecuación obtenemos:
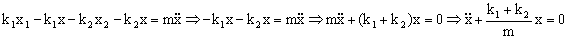
Como puede verse es la ecuación de un movimiento armónico simple. Para un único resorte la ecuación del movimiento será:
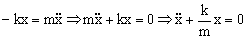
Tenemos también la ecuación de un movimiento armónico simple. Por comparación con la ecuación obtenida para los dos resortes, la constante equivalente será:
k=k1+k2=1+3=4 N/m
c) Hemos visto en el apartado anterior que el bloque realiza un movimiento armónico simple que responde a la ecuación:
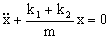
Por tanto la frecuencia angular será:
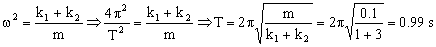
T=0.99 s