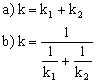
A lo largo de todo el problema tomaremos la dirección vertical como eje Y.
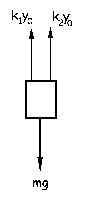
a) Inicialmente tenemos el sistema en equilibrio, teniendo ambos resortes la misma elongación que llamaremos y0. Como el sistema está en equilibrio:
ΣFy=0 ⇒ mg-k1y0-k2y0=0
A continuación desplazamos el bloque hacia abajo una cantidad y, y lo dejamos oscilar; los resortes, que antes estaban estirados una cantidad y0, ahora lo estarán y0+y. Aplicando la segunda ley de Newton:
Teniendo en cuenta la condición de equilibrio:
mg-k1y0-k2y0=0
Nos queda la ecuación:
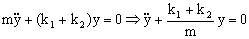
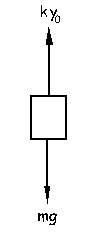Vamos a ver qué ocurre si sustituimos los dos resortes por un único resorte de constante k. Suspendemos de este resorte el mismo cuerpo de masa m, con lo cual el resorte se alargará una cantidad y0 y permanecerá en reposo. Para esta situación de equilibrio se cumplirá:
ΣFy=0 ⇒ mg-ky0=0
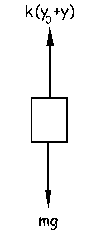A continuación desplazamos la masa m una cantidad y hacia abajo y la dejamos oscilar. Ahora tendremos:
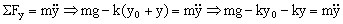
Teniendo en cuenta la condición de equilibrio que hemos obtenido antes:
mg-ky0=0
Nos queda la ecuación:
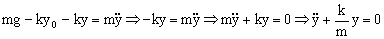
Donde podemos ver que tenemos también la ecuación de un movimiento armónico simple. Para que la ecuación sea igual que la que hemos obtenido para los dos resortes se deberá cumplir que:
k=k1+k2
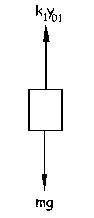b) Para el cuerpo en la posición de equilibrio tendremos lo que aparece en la figura. Como el sistema está en equilibrio:
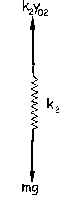Si aislamos el resorte 2 nos queda:
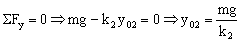
Sumando las dos ecuaciones tendremos:
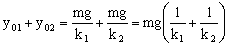
Ahora tenemos que sustituir ambos resortes por uno equivalente de constante k. Este resorte será equivalente si bajo el mismo cuerpo de masa m se alarga la misma cantidad, es decir:
y0=y01+y02
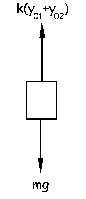Para este resorte en la posición de equilibrio tendremos lo que aparece en la figura. Como el cuerpo está en equilibrio:
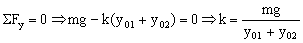
Sustituyendo la suma de alargamientos por el valor que hemos obtenido anteriormente:
