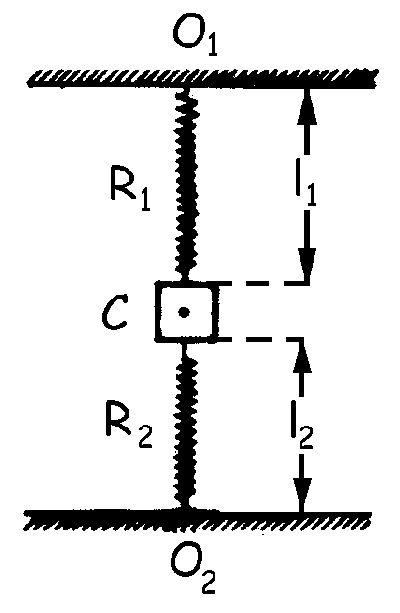
a) O2C=34 cm
b) y=-3cos15.65t
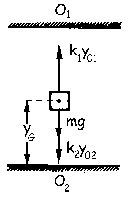 a) Llamaremos Y al eje en que se produce el movimiento (eje vertical).
a) Llamaremos Y al eje en que se produce el movimiento (eje vertical).
Para la posición de equilibrio tenemos lo que aparece en el diagrama. Como el sistema está en equilibrio se cumplirá:
ΣFy=0 ⇒ mg+k2y02-k1y01=0 ⇒ 0.2 · 9.8+24.5y02-24.5y01=0
1.96+24.5y02-24.5y01=0
Y además tendremos que:
O1O2=y01+l0+h+y02+l0 ⇒ 0.76=y01+0.25+0.04+y02+0.25 ⇒ y01+y02=0.22
Tenemos un sistema de dos ecuaciones y dos incógnitas:
1.96+24.5y02-24.5y01=0
y01+y02=0.22
De la segunda ecuación:
y01+y02=0.22 ⇒ y01=0.22-y02
Y sustituyendo en la primera:
1.96+24.5y02-24.5y01=0 ⇒ 1.96+24.5y02-24.5(0.22-y02)=0 ⇒ 49y02-3.43=0
y02=0.07 m
Y la otra elongación entonces:
y01=0.22-y02=0.22-0.07=0.0.15 m
Por tanto la altura del centro de gravedad del cilindro podemos ver que es:
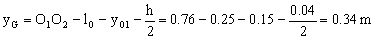
yG=0.34 m
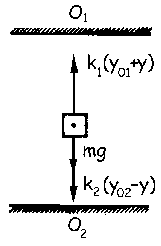 b) A continuación desplazamos hacia abajo el bloque C una cantidad «y» y lo dejamos oscilar. Tendremos el sistema que aparece en la figura. Aplicando la segunda ley de Newton:
b) A continuación desplazamos hacia abajo el bloque C una cantidad «y» y lo dejamos oscilar. Tendremos el sistema que aparece en la figura. Aplicando la segunda ley de Newton:
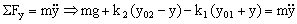
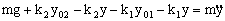
Teníamos ya de la condición de equilibrio:
mg+k2y02-k1y01=0
Luego eliminando estos términos que son nulos:
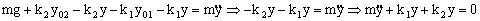
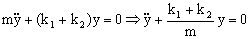
Tenemos la ecuación de un movimiento armónico simple de frecuencia angular:
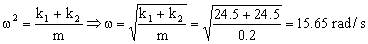
Como el bloque realiza un movimiento armónico simple, la ecuación de su posición será del tipo:
y=Asen(ωt+φ0)
donde A es la amplitud, ω la frecuencia angular y φ0 la fase inicial. La amplitud, que es el máximo desplazamiento, es de 3 cm:
A=3 cm
Para la fase inicial sabemos que cuando t=0 ⇒ y=A, luego sustituyendo esta condición en la ecuación:
y=Asen(ωt+φ0) ⇒ A=Asenφ0 ⇒ senφ0=1 ⇒ φ0=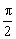
Con lo cual nos queda la ecuación:

y=3cos15.65t