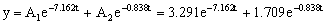a) k=29.92 N/m
b) a=12.27 m/s2
c) x=3.29 e-7.162t+1.709 e-0.838t
a) Los períodos de las distintas masas, se obtienen dividiendo entre 100 el tiempo correspondiente a las 100 oscilaciones:
|
T (s) |
1.153 |
1.6225 |
1.987 |
3.035 |
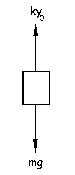 Tenemos un resorte vertical. Para la posición de equilibrio el sistema está como aparece en la figura. Si denominamos eje Y a la dirección del movimiento:
Tenemos un resorte vertical. Para la posición de equilibrio el sistema está como aparece en la figura. Si denominamos eje Y a la dirección del movimiento:
ΣFy=0 ⇒ mg-ky0=0
Ahora desplazamos el bloque una distancia y hacia abajo y lo dejamos oscilar libremente. Durante el movimiento:
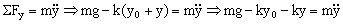
De la condición de equilibrio teníamos que: ΣFy=0 ⇒ mg-ky0=0.
Si eliminamos estos términos de la ecuación diferencial : 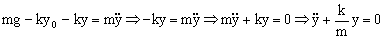 Nos queda la ecuación de un movimiento armónico simple de frecuencia angular:
Nos queda la ecuación de un movimiento armónico simple de frecuencia angular: 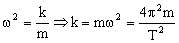
Y podemos determinar la constante correspondiente a cada masa y período:
|
k (N/m) |
29.70 |
29.99 |
30.0 |
30.0 |
Haciendo una media aritmética: 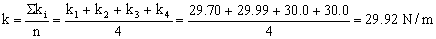
b) Para la masa de 5 kg la frecuencia angular será: 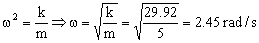 .
.
Como tenemos un movimiento armónico simple, la ecuación que nos da la posición de la partícula en función del tiempo es:
y=Asen(ωt+φ0)
En la posición de equilibrio tenemos que y=0 luego nos queda la ecuación:
y=Asen(ωt+φ0) ⇒ 0= Asen(ωt+φ0) ⇒ sen(ωt+φ0)=0 ⇒ cos(ωt+φ0)=1
La velocidad es la derivada del espacio respecto del tiempo: 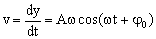 .
.
Teniendo en cuenta el valor del coseno en ese momento:
v=Aωcos(ωt+φ0)=Aω
Sabemos que en esa posición la velocidad es de 5 m/s luego: 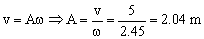 . Ahora en el punto de máxima elongación tendremos que: y=A
. Ahora en el punto de máxima elongación tendremos que: y=A
Aplicando esta condición:
y=Asen(ωt+φ0) ⇒ A=Asen(ωt+φ0) ⇒ sen(ωt+φ0)=1
La aceleración es la derivada de la velocidad respecto del tiempo: 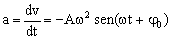 . Teniendo en cuenta el valor del seno en esta posición:
. Teniendo en cuenta el valor del seno en esta posición:
a=-Aω2sen(ωt+φ0)=-Aω2=-2.04 · 2.452=-12.27 m/s2..
Y en módulo:
a=12.27 m/s2
c) La fuerza de amortiguamiento es proporcional a la velocidad y vale 100 N cuando la velocidad es de 2.5 m/s:
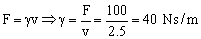
El parámetro de amortiguamiento será: 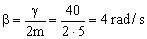 . La frecuencia angular de la oscilación sin amortiguar es: ω0=2.45 rad/s. Como ω0<β, el movimiento es sobreamortiguado, luego la ecuación que lo rige es:
. La frecuencia angular de la oscilación sin amortiguar es: ω0=2.45 rad/s. Como ω0<β, el movimiento es sobreamortiguado, luego la ecuación que lo rige es: 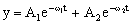
siendo 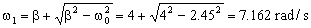 y
y 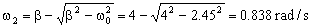
Tenemos entonces la ecuación: 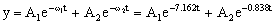 . Nos falta determinar las constantes A1 y A2. Para ello sabemos que cuando t=0 ⇒ y=5 m ⇒ v=-25 m/s. Aplicando la primera condición:
. Nos falta determinar las constantes A1 y A2. Para ello sabemos que cuando t=0 ⇒ y=5 m ⇒ v=-25 m/s. Aplicando la primera condición: 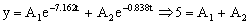
Para aplicar la condición de la velocidad tenemos que determinar primero la expresión de la misma. Derivando la ecuación de la elongación respecto del tiempo:
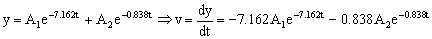
Sabemos que cuando t=0 ⇒ v=-25 m/s luego nos queda:
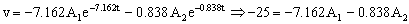
Tenemos un sistema de dos ecuaciones y dos incógnitas:
5=A1+A2
25=7.162A1+0.838A2
De la primera ecuación: 5=A1+A2 ⇒ A1=5-A2. Y sustituyendo en la segunda:
25=7.162A1+0.838A2 ⇒ 25=7.162(5-A2)+0.838A2 ⇒ 25=35.81-7.162A2+0.838A2
10.81=6.324A2 ⇒ A2=1.709 m
Y la otra constante A1: A1=5-A2=5-1.709=3.291 m
Luego la ecuación del movimiento es: