a) movimiento armónico simple; y=-0.1cos2.21t
b) movimiento subamortiguado; y=0.1 e^-0.0049tcos2.21t
c) movimiento amortiguado crítico; y=(0.1+0.221t)e^-2.21t
d) ω=2.21 rad/s; A=113 m

a) Denominaremos eje Y al eje en que se produce el movimiento, es decir, a la dirección vertical. La masa del cuerpo será:

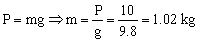
Para la posición de equilibrio tendremos lo que aparece en el gráfico adjunto. Como el peso está en reposo se cumplirá que:

ΣF_y=0 ⇒ mg-ky₀=0

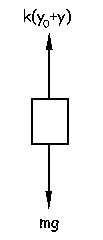A continuación desplazamos el bloque hacia abajo una cantidad y, y lo dejamos oscilar. Aplicando la segunda ley de Newton:

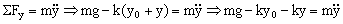
Sabemos por la condición de equilibrio que:

mg-ky₀=0

Eliminando estos términos de la ecuación:

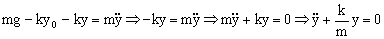
Es la ecuación de un movimiento armónico simple de frecuencia angular:

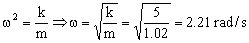
Como tenemos un movimiento armónico simple la solución de la ecuación es del tipo:

y=Asen(ωt+φ₀)

La amplitud nos dicen que es de 10 cm:

A=10 cm=0.1 m

Además tenemos que cuando t=0 ⇒ y=-A, luego aplicando esta condición:

La ecuación que nos da la posición en función del tiempo es entonces:

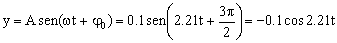
y=-0.1cos2.21t

 

b) Añadiendo el término correspondiente al rozamiento, la ecuación diferencial del movimiento será ahora:

donde la constante que acompaña a la velocidad es:

γ=0.01 Ns/m

También podemos expresar la ecuación diferencial como:

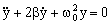
La frecuencia natural del oscilador es:

ω₀=2.21 rad/s

Ahora tenemos que determinar el tipo de amortiguamiento. Para ello debemos calcular el parámetro de amortiguamiento, que será:

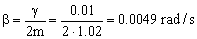
Como β < ω₀ el movimiento es subamortiguado, y la solución de la ecuación será:

y=A₀e^-βtcosωt

En esta ecuación A₀ es la amplitud inicial, que vale:

A₀=0.1 m

Y la frecuencia será:

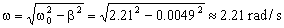
Entonces tenemos que la ecuación que nos da la posición del bloque en función del tiempo es:

y=A₀e^-βtcosωt=0.1e^-0.0049tcos2.21t

y= 0.1e^-0.0049tcos2.21t

 

c) Tendríamos el mismo caso que antes, movimiento amortiguado, pero la constante de amortiguamiento es diferente, y ahora vale:

γ=4.52 Ns/m

Por tanto el parámetro de amortiguamiento ahora es:

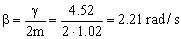
Como β=ω₀ el amortiguamiento es crítico, y la solución de la ecuación diferencial es:

y=(A₀+A₁t)e^-βt=(A₀+A₁t)e^-2.21t

Vamos a determinar las dos constantes que nos faltan, A₀ y A₁. En primer lugar sabemos que cuando t=0 ⇒ y=0.1 m luego:

y =(A₀+A₁t)e^-2.21t ⇒ 0.1=A₀

Ya tenemos una de las constantes, luego:

A₀=0.1 m ⇒ y=(A₀+A₁t)e^-2.21t=(0.1+A₁t)e^-2.21t

También sabemos que cuando t=0 el sistema parte del reposo, es decir, la velocidad es nula. La velocidad valdrá:

Aplicamos la condición de contorno de que cuando t=0 ⇒ :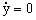

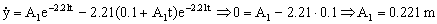
La ecuación correspondiente al movimiento es entonces:

y=(0.1+A₁t)e^-2.21t=(0.1+0.221t)e^-2.21t

y=(0.1+0.221t)e^-2.21t

 

d) Tenemos el caso b), luego el movimiento es subamortiguado, pero además se está ejerciendo una fuerza externa, luego también es forzado. Podemos determinar la frecuencia a la que se produce la resonancia, es decir, la frecuencia que debe tener la fuerza externa para que la amplitud de las oscilaciones sea máxima. Dicha frecuencia es:

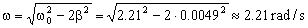
ω=2.21 rad/s

La fuerza externa es:

F=25·10⁴cosωt

es decir, es del tipo:

F=F₀cosωt

siendo:

F₀=25·10⁴ dinas=2.5 N

La amplitud correspondiente a la resonancia vale:

Como tenemos que ω₀ » ω:

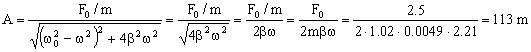
A=113 m