a) ω=12.78 rad/s
b) A=2 cm
c) P=0.0418 W
d) A=0.133 cm
e) P=0.740 mW
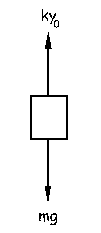 a) Tomaremos como eje Y el de la dirección del movimiento, es decir, el vertical. Aislamos el objeto y trazamos el diagrama de sólido libre. Para la posición de equilibrio el resorte se alarga 6 cm luego tenemos:
a) Tomaremos como eje Y el de la dirección del movimiento, es decir, el vertical. Aislamos el objeto y trazamos el diagrama de sólido libre. Para la posición de equilibrio el resorte se alarga 6 cm luego tenemos:
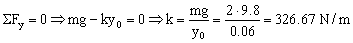
La frecuencia natural de la oscilación será por tanto:
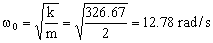
Y del factor de calidad podemos obtener el parámetro de amortiguamiento:

Como β<ω0 el movimiento es subamortiguado. La frecuencia de la resonancia es entonces:
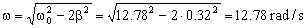
ω=12.78 rad/s
b) La amplitud correspondiente será:
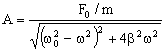
Como el movimiento es subamortiguado podemos ver que:
ω=ω0
luego tenemos:
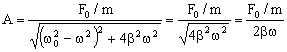
F0 es la fuerza externa máxima, luego se corresponde con la aceleración máxima. Dicha aceleración vale Aω2 luego tendremos:
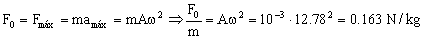
Sustituyendo:
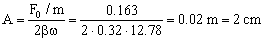
A=2 cm
c) La potencia será:
P=mβω2A2=2 · 0.32 · 12.782 · (2 · 10-2)2=0.0418 W
P=0.0418 W
d) La frecuencia de la fuerza impulsora es ahora:
ω=2ω0=2 · 12.78=25.56 rad/s
Cambiará también la aceleración máxima, luego cambia la fuerza F0:
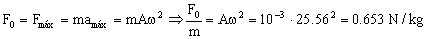
Y la amplitud correspondiente será ahora:
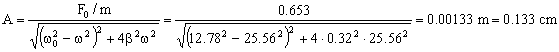
A=0.133 cm
e) Y la potencia:
P=mβω2A2=2·0.32·25.562 · 0.001332=0.000740 W=0.740 mW
P=0.740 mW