a_A=0.64 m/s²; a_B=1.59 m/s²

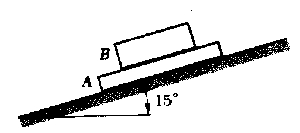
En este problema y en los dos siguientes se tendrá en cuenta que m_A=m_B=m=50 kg. Suponemos en principio que el bloque B no desliza respecto del A. En este caso:

a_A=a_B=a

Y además se debería cumplir que:

F_r<(F_r)_máx

 

Para el bloque B:

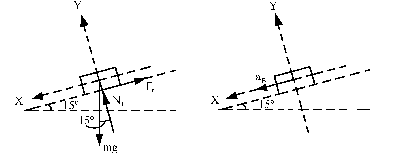
Aplicamos la segunda ley de Newton:

ΣF_X=ma_X ⇒ mgsen15^o-F_r=ma

∑F_Y=ma_Y ⇒ N_B-mgcos15^o=0 ⇒ N_B=mgcos15^o=50 × 9.8cos15⁰=473.3 N

(F_r)_máx=0.1N_B=0.1 × 473.3=47.33 N

Para el bloque A tendremos:

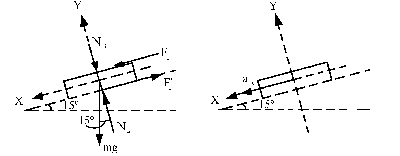
ΣF_X=ma_X ⇒ mgsen15^o+F_r-F_r´=ma

ΣF_Y=ma_Y ⇒ N_A-N_B-mgcos15^o=0 ⇒ N_A=N_B+mgcos15^o=473.3+50 × 9.8cos15^o=946.6 N

(F_r´)_máx=0.15N_A=0.15 × 946.6=142 N

Si el sistema se mueve como un solo bloque, el bloque A debe deslizar respecto del suelo luego:

F_r´=(F_r´)_máx=142 N

Y tendremos de la ecuación del eje X:

mgsen15^o+F_r-F_r´=ma ⇒ 50 × 9.8sen15^o+F_r-142=50a

Y de la ecuación del eje X del bloque B:

mgsen15^o-F_r=ma ⇒ 50 × 9.8sen15^o-F_r=50a

Como en ambas ecuaciones el segundo miembro es igual, el primero también debe serlo luego:

50 × 9.8sen15^o+F_r-142=50 × 9.8sen15^o-F_r ⇒ F_r=71 N

Habíamos dicho al principio que si el bloque B no desliza respecto de A debía cumplirse que:

F_r<(F_r)_máx

Como:

F_r=71 N; (F_r)_máx=47.33 N

Vemos que lo que hemos supuesto no es cierto, y los dos bloques deslizan entre sí. Como ahora sabemos que desliza tendremos que:

a_A≠a_B

Y además:

F_r=(F_r)_máx=47.33 N; F_r´=(F_r´)_máx=142 N

Ahora para el bloque A tendremos:

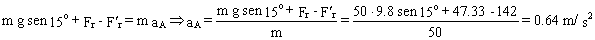
a_A=0.64 m/s²

 

Ahora para el bloque B:

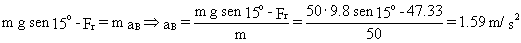
a_B=1.59 m/s²