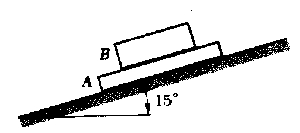
θ < 5.71^o no se mueve ningún bloque; 5.71^o < θ < 11.31^o desliza el bloque B; θ > 11.31^o deslizan ambos bloques

Si el ángulo θ es variable, para el bloque B nos quedará:

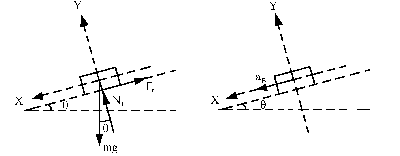
Sobre el eje vertical:

ΣF_Y=ma_Y ⇒ N_B-mgcosθ=0 ⇒ N_B=mgcosθ

El bloque B estará a punto de deslizar cuando la componente del peso, tangencial al plano inclinado, iguale a la fuerza de rozamiento máxima entre ambos bloques:

mgsenθ=fN_B ⇒ mgsenθ=fmgcosθ ⇒ tgθ=f=0.1 ⇒ θ=5.71^o

En el bloque A:

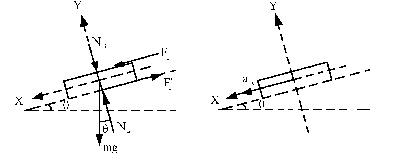
ΣF_Y=ma_Y ⇒ N_A-N_B-mgcosθ=0 ⇒ N_A=N_B+mgcosθ=mgcosθ+mgcosθ=2mgcosθ=

=2 ×50 ×9.8cos5.71^o=975.14 N

ΣF_X=ma_X ⇒ mgsenθ+0.1mgcosθ-F_r´=ma_A

Para que este bloque se mueva es necesario que mgsenθ+0.1mgcosθ supere a la fuerza de rozamiento existente entre A y el plano inclinado.

Para el ángulo de inclinación θ determinado antes de 5.71^o tenemos:

mgsenθ+0.1mgcosθ=50 ×9.8sen5.71^o+0.1 ×50 ×9.8cos5.71^o=97.5 N

(F_r´)_máx=0.15N_A=0.15 ×975.14=146.27 N

Por tanto el bloque A con esa inclinación del plano, no se mueve. Para ángulos inferiores a 5.71^o no se mueve ninguno de los dos bloques.

θ<5.71^o ⇒ No movimiento

A partir de aquí, al aumentar θ empezaría a deslizar el bloque B y se mantendría en reposo el A. Por último, el bloque A estará a punto de deslizar por el plano inclinado cuando:

mgsenθ+0.1mgcosθ>(F_r´)_máx ⇒ mgsenθ+0.1mgcosθ>0.15N_A ⇒

mgsenθ+0.1mgcosθ > 0.15 × 2mgcosθ > 0.3mgcosθ ⇒
senθ > 0.2cosθ ⇒ tgθ > 0.2 ⇒ θ < 11.31^O

Por tanto, para valores de θ ≤ 5.71^o no se mueve ningún bloque y para valores de θ
comprendidos entre 5.71^o y 11.3^o desliza B sobre A y éste permanece en reposo:

Para valores de θ superiores a 11.31^o deslizan los dos pero sus aceleraciones son diferentes.