a) a=15405.34 km
b) vBelip=9217.61 m/s
c) T=6.17 h
a) Para una órbita circular se tiene:
![]()
de donde se puede extraer la relación entre el radio r de la órbita y el periodo T de la misma:
![]()
En este caso, para un vehículo orbitando en torno a la Tierra, con periodo T = 10 h = 10.3600 = 36000 s, podemos obtener r:
![]()
A partir de la primera ecuación, la velocidad para una órbita circular tiene por expresión:
![]()
Particularizando para el vehículo en torno a la Tierra, la velocidad en todo punto, y por tanto en el punto A es:
![]()
Puesto que el vehículo sufre un D
v en el punto A:
![]()
siendo vi = vAcirc, y vf corresponderá con vAelip, ya que pasa a describir una órbita elíptica, como nos dicen. Así:
![]()
Para una órbita elíptica, puesto que siempre se da que ET = cte = Ec + Ep :
![]()
Particularizando para el vehículo en torno a la Tierra, en el punto A:
![]()
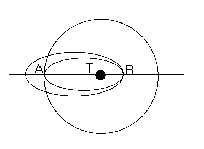
Puesto que rA coincide con el radio de la órbita circular, podemos despejar para obtener el valor de a:
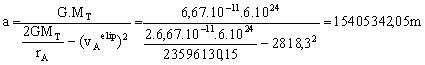
Por tanto:
![]()
b) Para calcular la velocidad en una órbita elíptica, aplicando también la ecuación ET=cte=Ec+Ep se tiene:
![]()
Particularizando para el vehículo en torno a la Tierra, en el punto B, aparece el valor rB. Este lo podemos calcular en términos de a y rA, ya que:
![]()
Con esto, tenemos ya, para la velocidad en el punto B:
![]()
Nota: también podíamos haber calculado vBelip a partir de la conservación del momento angular:
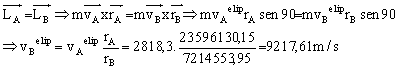
Por tanto:
![]()
c) La energía total de una masa m orbitando en torno a otra es, como ya hemos utilizado:
![]()
Una variación en la energía total lleva, por lo tanto, a una variación del semieje mayor:
![]()
Particularizando para el vehículo en torno a la Tierra, con el cambio de energía que nos dan, tenemos:
![]()
Conocido el semieje mayor de la nueva órbita, el periodo se calcula como:
![]()
Por tanto:
![]()