a) v=12.78 m/s
b) v=0.268 m/s
c) y=10-3sen(20.94x-267.66t)
d) P=0.0549 W
a) La velocidad de propagación de ondas transversales en una cuerda tensa viene dada por:
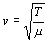
donde T es la tensión a que está sometida la cuerda y m su densidad lineal. En nuestro caso la cuerda está sometida únicamente a la carga de 2 kg luego la tensión será igual a este peso:
T=mg=2·9.8=19.6 N
Y la densidad lineal:
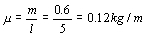
Por tanto la velocidad de propagación es:
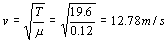
v=12.78 m/s
b) La ecuación general de la onda es:
y=Asen(kx-ωt)
La amplitud del movimiento es:
A=0.1 cm=10-3 m
El número de ondas:
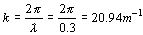
Y la frecuencia angular:
ω =kv=20.94·12.78=267.66 rad/s
Por tanto la ecuación de la onda será:
y=Asen(kx-ω t)=10-3sen(20.94x-267.66t)
y=10-3sen(20.94x-267.66t)
c) La velocidad de vibración de las partículas será:
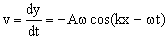
Esta velocidad será máxima cuando el término variable (coseno) adquiera su valor máximo, que es la unidad. Por tanto:
cos(kx-ωt)=1 ⇒ vmáx=-Aω =-10-3·267.66=-0.268 m/s
En módulo:
vmáx=0.268 m/s
d) El flujo energético promedio o potencia valdrá:
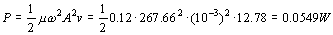
P=0.0549 W