1) ν’=632.21 s -1
2) ν»=539.50 s -1
1) Supondremos en todo el problema que tanto el globo como el tren pesan lo suficiente como para no ser arrastrados por el viento. La velocidad del viento por tanto sólo influirá en la velocidad de propagación de las ondas.
Para la situación inidial tendremos lo que se muestra en la figura.
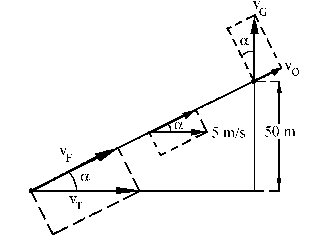
El observador estará situado en el globo y la fuente será el tren. Por geometría tendremos:

Como el sonido tiene que ir desde el tren hasta el globo, se verá favorecido por la velocidad del viento, de modo que la velocidad de las ondas será:
v=vS+5cosa =330+5cos26.57o=334.47 m/s
Tendremos entonces que por el efecto Doppler:
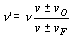
El observador se aleja y la fuente se acerca luego:

ν’=632.21 s-1
2) Veamos en primer lugar la situación al cabo de 10 s. Tanto el globo como el tren tienen movimiento rectilíneo y uniforme. El espacio recorrido por el tren será entonces:
sT=vTt=20·10=200 m
Como el tren estaba 100 m a la izquierda del globo y se desplaza 200 m hacia la derecha, quedará situado 100 m a la derecha del globo.
El espacio recorrido por el globo será:
sG=vGt=2·10=20 m
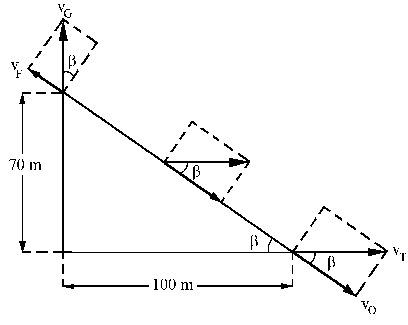
El globo estaba a 50 m de altura. Como se mueve 20 m hacia arriba, quedará a 70 m de altura, tal como muestra la figura.

El ángulo β valdrá:
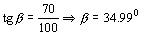
En primer lugar el sonido tiene que ir desde el tren hasta el globo. En esta primera parte el observador será el globo y la fuente el tren. El aire irá en contra del movimiento de las ondas, luego la velocidad real de las ondas será:
v=vS-5cosβ =330-5cos34.99o=325.90 m/s
La fuente emite una frecuencia ν y el observador percibe una frecuencia ν’. Teniendo en cuenta que tanto el observador como la fuente se alejan:
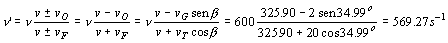
A continuación el sonido tiene que volver desde el globo hasta el tren. Supondremos que en el tiempo en que el sonido sube y baja las posiciones del globo y del tren no varían. En esta segunda parte, el observador será el tren, y la fuente será el globo, que emite con la misma frecuencia que ha recibido, es decir, con ν’.
Además, ahora el viento favorece la propagación de las ondas, luego la velocidad de propagación de las ondas será:
v=vS+5cosβ=330+5cos34.99o=334.10 m/s
Si tenemos en cuenta que de nuevo tanto la fuente como el observador se alejan entre sí nos quedará la ecuación del efecto Doppler:
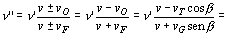
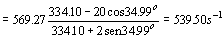
ν»=539.50 s-1