a) F=28.85 kg
b) Δl=2.5 mm; ΔV=1.24 mm³; E_Pe=0.353 J
c) F=57.7 kg

a) El esfuerzo máximo será el correspondiente al límite elástico:

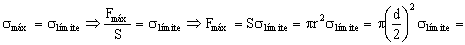
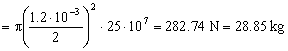
F_máx=28.85 kg

 

b) A partir del módulo de Young:

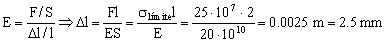
Δl=2.5 mm

Para determinar el cambio de volumen que experimenta el hilo tendremos que restar el volumen final menos el inicial:

ΔV=V_f-V₀

Inicialmente tendremos que el hilo es un cilindro, luego el volumen será el producto del área de la base (un círculo) por su altura (longitud del cilindro). En cuanto al volumen final tendremos que ha aumentado la longitud del hilo (l+Δl) y ha disminuido su radio (r+Δr). Hay que tener en cuenta que en los incrementos va incluído el signo, ya que el incremento supone la resta entre la magnitud final menos la inicial; por tanto, si la longitud aumenta Δl es positivo, mientras que como el radio disminuye Δr es negativo. La variación de volumen es:

ΔV=V_f-V₀=π(r+Δr)²(l+Δl)-πr²l=π(r²+Δr²+2rΔr)(l+Δl)-πr²l=

=πr²l+πΔr²l+2πrΔrl+πr²Δl+πΔr²Δl+2πrΔrΔl-πr²l=πΔr²l+2πrΔrl+πr²Δl+πΔr²Δl+2πrΔrΔl

Como la variación tanto de radio como de longitud, es muy pequeña, podemos despreciar infinitésimos de orden dos o superiores:

ΔV=2πrΔrl+πr²Δl

La variación de longitud es conocida, y las variación de radio podemos relacionarla con la de longitud a través del coeficiente de Poisson:

Sustituyendo en la ecuación que nos da la variación de volumen:

ΔV=1.24 mm³

Y la energía potencial elástica almacenada:

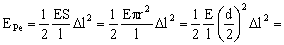
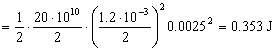
E_Pe=0.353 J

c) Para que no se supere el límite de rotura el esfuerzo máximo será:

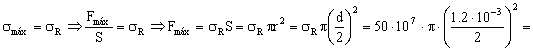
=565.49 N=57.7 kg

F_máx=57.7 kg