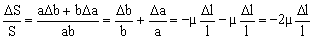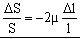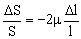
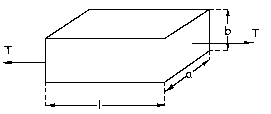
 Tendremos el paralelepípedo tal como muestra la figura. El módulo de Poisson es:
Tendremos el paralelepípedo tal como muestra la figura. El módulo de Poisson es:
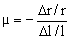
siendo r una dimensión perpendicular a l, por lo que nos valdrá para a y para b:
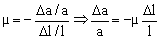
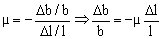
Buscamos la variación en la sección transversal 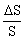 . La sección transversal es:
. La sección transversal es:
S=ab
Una vez aplicada la tensión, la sección final será:
S+ΔS=(a+Δa)(b+Δb)=ab+aΔb+Δab+ΔaΔb
Despreciamos los infinitésimos de orden superior a uno:
S+ΔS= ab+ aΔb+Δab
Por tanto:
ΔS=(S+ΔS)-S= ab+ aΔb+Δab-ab=aΔb+bΔa
Entonces la variación unitaria: