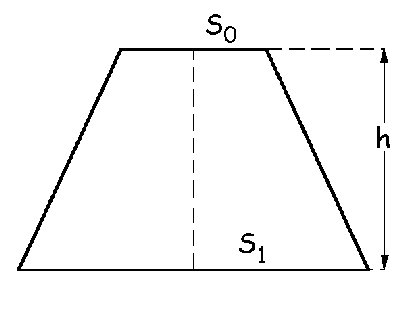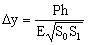
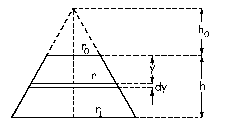
El tronco de cono es un cono al que se le ha cortado la parte superior. Podemos representar tal como muestra la figura, el cono completo, denominando h0 a la parte del cono que se ha eliminado. Obviamente, aunque este parámetro es constante, es desconocido y debemos eliminarlo de la solución final. Llamaremos r0 y r1 a los radios de las secciones S0 y S1 respectivamente. El acortamiento del tronco de cono no es igual en toda la altura, ya que varía la sección. Tomaremos por tanto un elemento diferencial, que será un disco de altura dy y radio r, y posteriormente integraremos para toda la altura.
Por geometría (triángulos semejantes) tendremos:
Nuestro elemento diferencial tiene una sección genérica S, situada a una distancia y de la base superior. Para esta sección también podemos escribir, por triángulos semejantes:
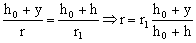
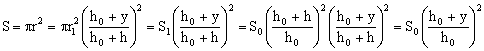
El elemento de tronco de cono de espesor dy y sección S sufre un acortamiento dΔy bajo la compresión P. Aplicando la definición de módulo de Young a este elemento diferencial tendremos:
Integrando esta expresión tendremos el acortamiento del tronco de cono:
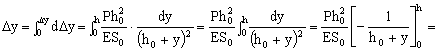
Teníamos al principio:
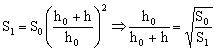
Sustituyendo:
