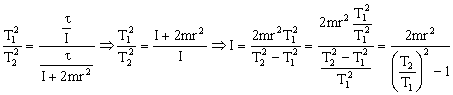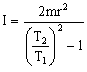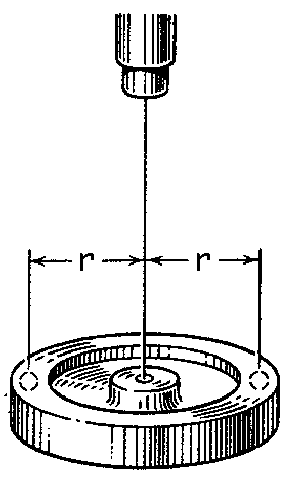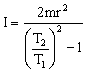
Al girar el volante el alambre se retuerce y reacciona sobre el disco produciendo un par de sentido contrario al ángulo girado y proporcional a él que vale en módulo:
M=τθ
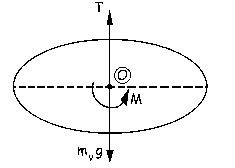 Si aislamos el volante cuando está sin las masas adicionales y tomamos momentos con respecto a un eje perpendicular al volante que pase por su centro geométrico O, que coincide con su centro de masa, tendremos que no dan momento ni la tensión ni el peso del volante, por ser paralelas al eje, y sólo nos queda:
Si aislamos el volante cuando está sin las masas adicionales y tomamos momentos con respecto a un eje perpendicular al volante que pase por su centro geométrico O, que coincide con su centro de masa, tendremos que no dan momento ni la tensión ni el peso del volante, por ser paralelas al eje, y sólo nos queda:
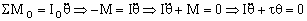
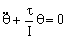
Tenemos la ecuación de un movimiento armónico simple del tipo:
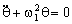
Por tanto la frecuencia angular de este movimiento es:
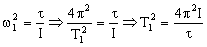
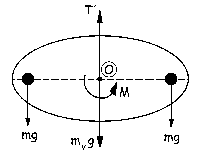 A continuación añadimos las masas adicionales sobre el volante, lo giramos un ángulo θ y lo dejamos oscilar. Realizamos como antes el diagrama de sólido libre, que es el de la figura. El par M sigue siendo proporcional al ángulo girado y con la misma constante de proporcionalidad, ya que el alambre no ha cambiado. Con respecto al eje perpendicular al volante que pasa por O no dan momento ni la tensión ni los pesos, ya que todas estas fuerzas son perpendiculares al eje. Tendremos entonces:
A continuación añadimos las masas adicionales sobre el volante, lo giramos un ángulo θ y lo dejamos oscilar. Realizamos como antes el diagrama de sólido libre, que es el de la figura. El par M sigue siendo proporcional al ángulo girado y con la misma constante de proporcionalidad, ya que el alambre no ha cambiado. Con respecto al eje perpendicular al volante que pasa por O no dan momento ni la tensión ni los pesos, ya que todas estas fuerzas son perpendiculares al eje. Tendremos entonces:
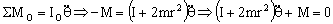
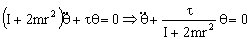
Tenemos otra vez la ecuación de un movimiento armónico simple del tipo:
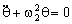
La nueva frecuencia angular es:
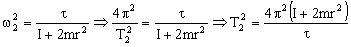
Dividiendo los dos períodos: