n´=1.96
Tendremos lo que aparece en la figura. No tendremos en cuenta la reflexión, sino sólo la refracción. Aplicamos la ley de Snell a la primera de las refracciones, que va del aire al vidrio:
nsenθi=n´senθr
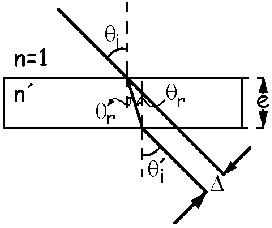 En la segunda refracción, que va del vidrio al aire, el ángulo de incidencia es el que antes era de refracción, θr, y llamaremos θ´i al ángulo de refracción. Aplicando de nuevo la ley de Snell:
En la segunda refracción, que va del vidrio al aire, el ángulo de incidencia es el que antes era de refracción, θr, y llamaremos θ´i al ángulo de refracción. Aplicando de nuevo la ley de Snell:
n´senθr=nsenθ´i
Vemos que el segundo miembro de la primera ecuación es igual al primer miembro de esta segunda ecuación, por lo que se deduce que:
nsenθi=nsenθ´i ⇒ senθi=senθ´i ⇒ θi=θ´i

Esto demuestra que el rayo emergente es paralelo al incidente, pero sufre un desplazamiento lateral. Vamos a relacionar ahora el desplazamiento lateral con los ángulos de incidencia y refracción. En la figura puede verse ampliada la parte del interior de la lámina, para ver mejor los ángulos y las distancias. El triángulo ADC es un triángulo rectángulo al cual le podemos aplicar el teorema del seno, de manera que se cumple que:


El triángulo ABC también es triángulo, y aplicamos también el teorema del seno, obteniéndose:
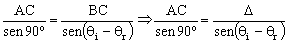
Podemos ver que los primeros miembros son iguales luego los segundos también lo serán:

Desarrollamos el seno de una resta, que es:
sen(a-b)=senacosb-cosasenb
Nos queda entonces:

14.142cosθr-14.142senθr=8.67cosθr ⇒ 14.142senθr=5.472cosθr
Teniendo en cuenta que:
sen2θrcos2θr=1 ⇒ 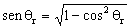
Sustituimos esto en la expresión que teníamos:

Elevando los dos miembros al cuadrado:
200(1-cos2θr)=30cos2θr ⇒ 200-200cos2θr=30cos2θr
200=230cos2θr ⇒ cosθr=0.933
θr=21.171º
Conocidos los ángulos de incidencia y refracción aplicamos la ley de Snell a la primera refracción:
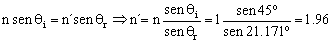
n´=1.96