a) Ti=18.95 oC
b) dos mínimos y tres máximos
Tenemos interferencias en el punto O no debido a que las ondas recorran caminos diferentes, ya que recorren 10 m en las dos ramas, sino debido a que las recorren con velocidades diferentes. Como la temperatura en las dos ramas es distinta, la velocidad será también distinta, ya que depende de la temperatura, y será distinto por tanto el tiempo que emplea cada onda en recorrer cada rama del aparato. Para que se produzca un mínimo el desfase debe ser igual a un número impar de veces π:
δ=(2n+1)π
Nos piden la temperatura de la rama inferior a la cual se produce el primer mínimo. El primer número impar es el uno, luego el primer mínimo se producirá cuando:
δ=π
Este desfase vale: kr-k´r=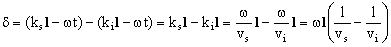
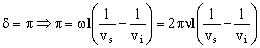
La velocidad del sonido en la rama superior es:
![]()
siendo ϒ el coeficiente adiabático de los gases, R la constante de los gases perfectos, Ts la temperatura en la rama superior y M la masa molecular del gas. De modo análogo, la velocidad del sonido en la rama inferior es:
![]()
Dividiendo las dos expresiones:
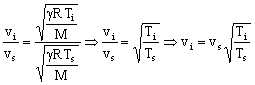
Sustituimos esto en la ecuación que tenemos para el desfase:
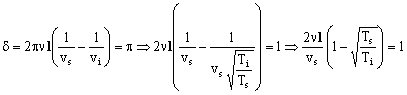
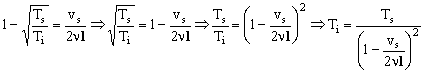
La temperatura de la rama superior se mantiene constante e igual a 0ºC luego:
Ts=0ºC=273 K
Conocemos la velocidad del sonido en aire a 0ºC, de manera que la velocidad del sonido en la rama superior es:
vs=330 m/s
Sustituyendo todo:
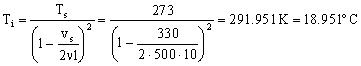
Ti=18.951ºC
b) Vamos a ver cuántos mínimos se producen al calentar el aire de la rama inferior entre 0ºC y 100ºC.
Habíamos determinado en el apartado anterior que el desfase es:
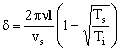
Su valor depende de la temperatura Ti de la rama inferior que es la única variable. Al ir aumentando esta temperatura, el valor de δ aumenta.
Para un valor de Ti=100 oC=373 K:
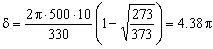
Tendremos un máximo o mínimo cuando el desfase, δ, sea igual a un múltiplo entero par o impar de veces π respectivamente.
Al ir subiendo la temperatura de la rama inferior de 0ºC a 100ºC, vamos a encontar para δ todos los valores comprendidos entre 0 y 4.38.
Por lo tanto tendremos:
3 MAXIMOS (δ=0, 2π y 4π)
y
2 MÍNIMOS (δ=π y 3π)
