Δl=38.8 μm
Vamos a ver en primer lugar en qué consiste un interferómetro de Michelson. El esquema de dicho aparato está en la figura.
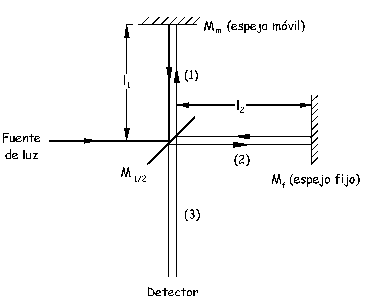
En este interferómetro, un haz de luz monocromático que procede de una fuente incide sobre un espejo, M1/2, que forma un ángulo de 45º con la dirección del haz. El recubrimiento de plata de este espejo tiene un espesor tal que refleja la mitad del haz incidente y transmite la otra mitad. Así, la mitad de la luz incidente se dirige hacia un espejo móvil, Mm, [haz (1)]
y la otra mitad se dirige hacia un espejo fijo Mf [haz (2)], y ambos espejos vuelven a reflejar la luz hacia M1/2, donde de nuevo la mitad de cada haz se transmite y la otra mitad se refleja. Nos fijamos en las partes de cada haz que se combinan para formar el haz (3) y luego se propagan hacia el detector.
El haz (3) está formado por ondas que han recorrido distancias distintas. Estas ondas pertenecen al haz (1), que ha recorrido 2l1, y al haz (2), que ha recorrido 2l2. La diferencia de distancias entre los dos haces es:
Δr=2l2-2l1=2(l2-l1)
Esta diferencia de caminos recorridos provoca un desfase entre las ondas que llegan al detector. Se observará un máximo cuando las ondas interfieran constructivamente, es decir, cuando el desfase entre ellas sea igual a un número par de veces π:
![]()
Supongamos ahora que desplazamos el espejo móvil Mm. La diferencia de caminos ha variado, de manera que ya no se percibe un máximo, sino una situación intermedia. Llegará otra posición del espejo móvil para la cual la distancia al centro del sistema sea l´2 tal que se vuelva a percibir un máximo en el detector, que será el máximo siguiente. En este caso se cumplirá que:
![]()
Si restamos las dos expresiones obtenidas:
![]()
En esta expresión la diferencia l´2-l2 es la distancia que hemos movido el espejo móvil para ver dos máximos consecutivos. En el problema nos dicen que al mover el espejo una cierta cantidad se observan 140 franjas de interferencias, luego tendremos:
![]()
Δl2=36.8 µm