a) a=54.25 nm
b) θ= 57.21^o

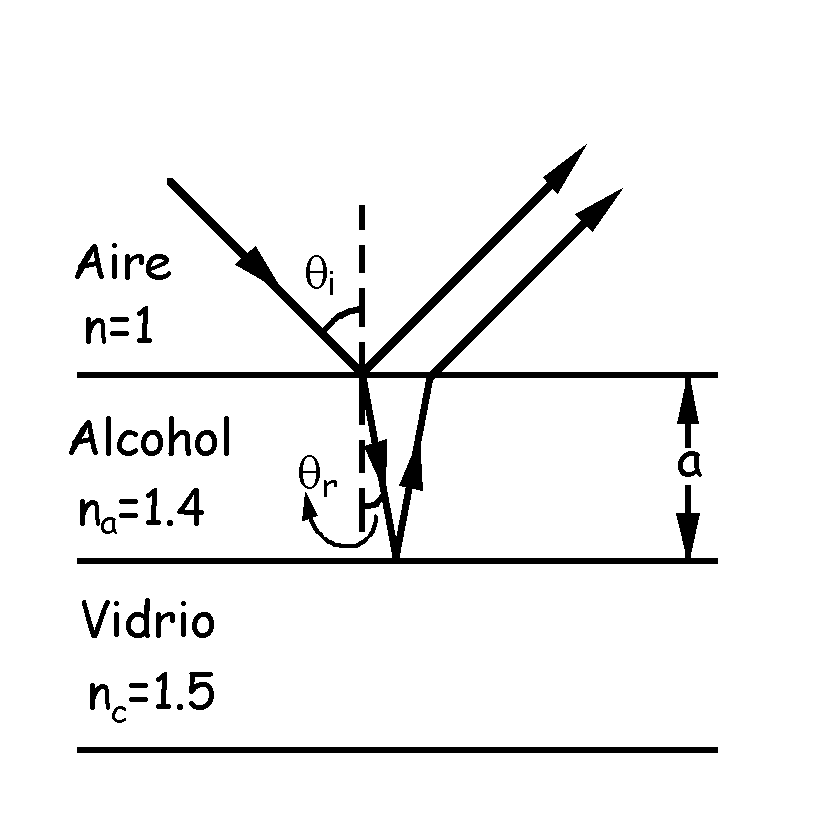a) Tenemos el sistema que aparece en la figura. Se producen interferencias entre los rayos reflejados en la cara superior de la lámina de alcohol y los reflejados en la cara inferior de la misma. Como la película presenta bandas oscuras lo que tenemos son mínimos de interferencia. Para que se produzcan mínimos el desfase entre las ondas tiene que ser igual a un número impar de veces π. En el desfase habrá que tener en cuenta los desfases adicionales que aparecen en las reflexiones, en nuestro caso, dos, en la cara superior y en la inferior de la lámina de alcohol. Teniendo en cuenta todo esto:

donde hemos eliminado el término 2π del primer miembro porque es un desfase igual a 0º y no influirá en el resultado final.

Como la incidencia es normal:

θ_i=0º

Aplicando la ley de Snell:

nsenθ_i=n_asenθ _r ⇒ nsen0º=n_asenθ_r ⇒ 0=n_asenθ_r ⇒ senθ_r=0 ⇒ θ_r=0º ⇒ cosθ_r=cos0º=1

Entonces:

Tenemos dos mínimos consecutivos, ya que entre medias de las dos longitudes de onda dadas no se observan más mínimos. Entonces, si uno es el mínimo de orden N, el otro será de orden (N+1), de manera que para las dos longitudes de onda se cumplirá:

Como los primeros miembros son iguales los segundos también lo serán:

1215.2N+607.6=868N+1302 ⇒ 347.2N=694.4 ⇒ N=2

Y sustituimos el valor de N en una cualquiera de las ecuaciones:

a=542.5 nm

Podemos comprobar que obtenemos el mismo resultado con la otra ecuación:

b) Nos piden el mínimo ángulo de incidencia para el que pueden observarse franjas oscuras por reflexión. Como la condición es la misma que antes, llegaríamos a la misma ecuación, pero ahora la incidencia no es normal; obtenemos pues:

Nos piden el ángulo de incidencia, luego tendremos que aplicar la ley de Snell, ya que en esa ecuación lo que nos aparece es el ángulo de refracción:

nsenθ_i=n_asenθ_r

Buscamos el mínimo ángulo de incidencia. Al aumentar el ángulo de incidencia aumenta el seno de este ángulo, de manera que el mínimo ángulo de incidencia debe ser el mínimo senθ_i. En la ley de Snell vemos que si senθ_i es mínimo senθ_r también lo será, lo que implica que el cosθ_r debe de ser máximo. Por tanto la condición del problema es que cosθ_r sea máximo, siempre cumpliéndose la condición de bandas oscuras:

Lo que haremos pues es dar valores enteros a N, para buscar el máximo valor del cosθ_r que cumple esta ecuación. Tendremos entonces:

Este último valor ya no es válido, puesto que el coseno de un ángulo no puede ser mayor de la unidad. El máximo valor del coseno que cumple la ecuación de las bandas oscuras es:

cosθ_r=0.7996 ⇒ θ_r=36.91º

Y aplicando la ley de Snell determinamos el ángulo de incidencia correspondiente:

θ_i=57.21º

>