Nmáx=134; a1=0; a2=300 nm; a3=600 nm……….a133=399·102 nm
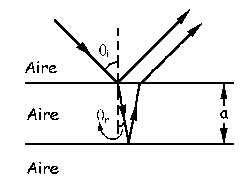 En este caso tenemos una lámina de aire de espesor variable pero el problema es únicamente las interferencias producidas en una lámina delgada. La única variación es la geometría. Nos dicen que se producen máximos de interferencia. La condición de máximo es que el desfase sea igual a un número par de veces π, de modo que tendremos:
En este caso tenemos una lámina de aire de espesor variable pero el problema es únicamente las interferencias producidas en una lámina delgada. La única variación es la geometría. Nos dicen que se producen máximos de interferencia. La condición de máximo es que el desfase sea igual a un número par de veces π, de modo que tendremos:
![]()
El sistema se ilumina normalmente luego el ángulo de incidencia es nulo. Aplicando la ley de Snell:
nsenθi=nsenθr ⇒ nsen0º=nsenθr ⇒ 0=nsenθr ⇒ senθr=0 ⇒ θr=0º ⇒ cosθr=cos0º=1
Nos queda entonces:
![]()
Como la película es de aire su índice de refracción es la unidad (n=1):
![]()
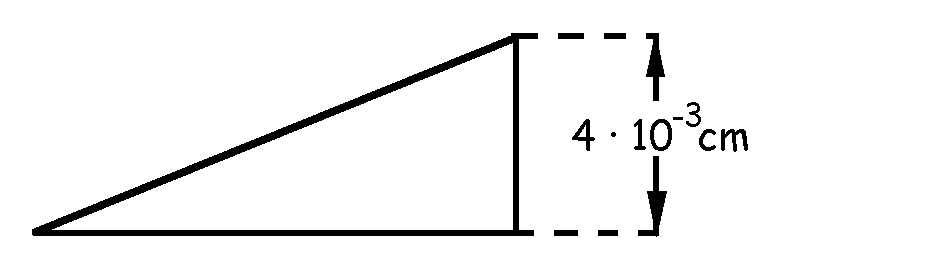 Como podemos ver, para distintos valores de N el valor del espesor será diferente. Cuanto mayor es N más grande es el espesor de la lámina. Para N=0 tendremos que a=0, y la primera franja brillante estará en el vértice. Para N=1 obtendremos otro espesor a1 que se corresponderá con la segunda franja; para N=2 tendremos un nuevo espesor a2 que nos dará la tercera franja. La última franja se obtendrá cuando el espesor sea lo más grande posible, es decir, en el extremo de la lámina. Para este espesor:
Como podemos ver, para distintos valores de N el valor del espesor será diferente. Cuanto mayor es N más grande es el espesor de la lámina. Para N=0 tendremos que a=0, y la primera franja brillante estará en el vértice. Para N=1 obtendremos otro espesor a1 que se corresponderá con la segunda franja; para N=2 tendremos un nuevo espesor a2 que nos dará la tercera franja. La última franja se obtendrá cuando el espesor sea lo más grande posible, es decir, en el extremo de la lámina. Para este espesor:
![]()
Vemos que no es un número entero, y N sólo puede tomar valores enteros. Esto significa que ese espesor no es justo el de un máximo, sino que está entre medias. El último máximo se formará con N=133, que se corresponderá con un espesor:
![]()
Este espesor será a133, lo que implica que contando la franja del vértice es el máximo número 134:
134 FRANJAS
Los espesores a los que se producirán los máximos serán los que verifiquen la condición:
![]()
Por tanto no tenemos más que dar valores enteros a N para ir obteniendo los espesores correspondientes. Tendremos:
![]()
a1=0
![]()
a2=300 nm
![]()
a3=600 nm
![]()
a4=900 nm
Y así sucesivamente, un máximo cada vez que el espesor de la lámina aumenta 300 nm.