r =0.11 cm
En primer lugar determinaremos el radio de la lente R, a través de la ecuación de las lentes:
![]()
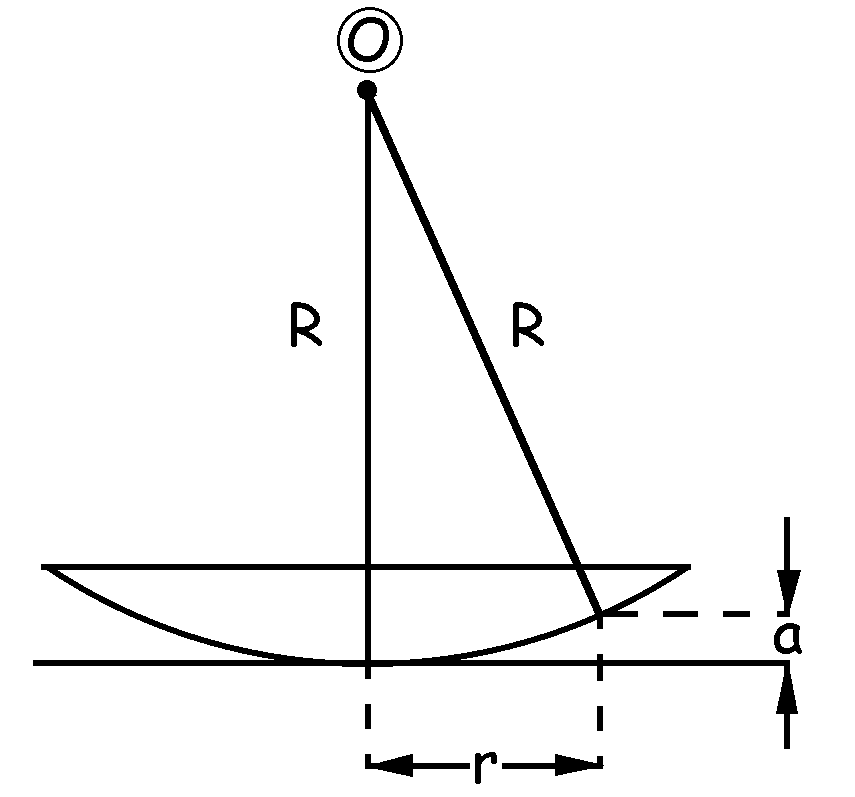 Tendremos el esquema que aparece en la figura. Como puede verse, entre la lente y la lámina de vidrio se forma una capa de aire de espesor a variable. Dependiendo de lo que valga este espesor se producirán interferencias constructivas y destructivas, de modo que aparecerán máximos y mínimos. El espesor a es el mismo para una circunferencia de radio r alrededor de la lente, de manera que las bandas tienen forma circular con radio r. Dichas bandas son las llamadas anillos de Newton. Nos dicen que se producen máximos, luego el desfase entre las ondas tiene que ser igual a un número par de veces π. Tendremos entonces:
Tendremos el esquema que aparece en la figura. Como puede verse, entre la lente y la lámina de vidrio se forma una capa de aire de espesor a variable. Dependiendo de lo que valga este espesor se producirán interferencias constructivas y destructivas, de modo que aparecerán máximos y mínimos. El espesor a es el mismo para una circunferencia de radio r alrededor de la lente, de manera que las bandas tienen forma circular con radio r. Dichas bandas son las llamadas anillos de Newton. Nos dicen que se producen máximos, luego el desfase entre las ondas tiene que ser igual a un número par de veces π. Tendremos entonces:
![]()
La luz incide por encima de la cara plana. Supondremos que la incidencia es normal, de modo que el ángulo de incidencia es nulo. Aplicando la ley de Snell:
nsenθi=nsenθr ⇒ nsen0º=nsenθr ⇒ 0=nsenθr ⇒ senθr=0 ⇒ θr=0º ⇒ cosθr=cos0º=1
Con lo cual nos queda:
![]()
La lámina que provoca la interferencia es una lámina de aire, luego su índice de refracción es la unidad (n=1):
![]()
Como puede verse, al aumentar N aumenta a. Para N=0 tendremos que el espesor a es nulo, lo que ocurre en el centro de la lente, y tendremos un punto brillante. Para N=1 obtenemos un cierto espesor, y por tanto un radio r, en el que aparecerá el primer anillo de Newton. El séptimo anillo de Newton se producirá cuando N=7:
2a=Nλ ⇒ 2a=7λ
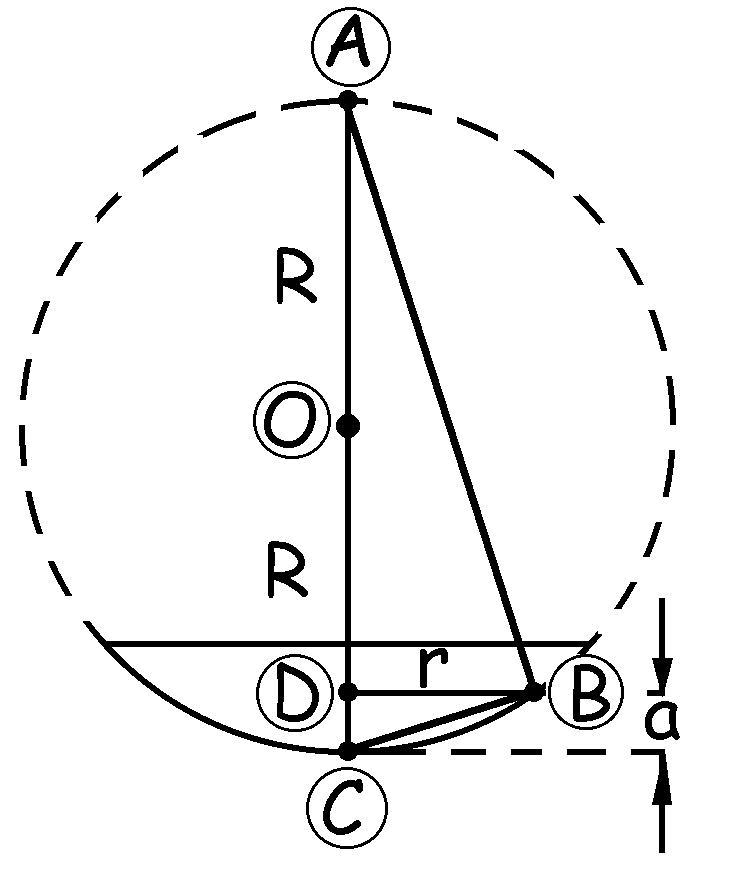 Ahora nos falta relacionar el espesor a de la capa de aire con el radio r del anillo de Newton correspondiente. Para ello dibujamos la lente de radio R y marcamos el espesor a y el radio r. En el triángulo ABC se cumplirá:
Ahora nos falta relacionar el espesor a de la capa de aire con el radio r del anillo de Newton correspondiente. Para ello dibujamos la lente de radio R y marcamos el espesor a y el radio r. En el triángulo ABC se cumplirá:
AC2=AB2+BC2 ⇒ (DC+DA)2=AB2+BC2
En el triángulo ABD se cumple:
AB2=BD2+DA2 ⇒ DA2=AB2-BD2
Y en el triángulo DBC:
BC2=DC2+BD2 ⇒ DC2=BC2-BD2
Sumamos estas dos últimas ecuaciones:
DA2+DC2= AB2-BD2+ BC2-BD2 ⇒ DA2+DC2= AB2+BC2-2BD2
Sustituimos AB2+BC2 por el valor que hemos obtenido del triángulo ABC y nos queda:
DA2+DC2=AB2+BC2-2BD2 ⇒ DA2+DC2=(DC+DA)2-2BD2 ⇒
DA2+DC2=DC2+DA2+2DC · DA-2BD2
Simplificando:
0=2DC · DA-2BD2 ⇒ 0=DC · DA-BD2 ⇒ BD2=DC · DA ⇒ r2=a(R-a)
Desarrollando el paréntesis:
r2=a(2R-a) ⇒ r2=2aR-a2
Como el espesor a de la película es muy pequeño podemos despreciar a2 frente a los otros términos y nos queda:
![]()
Vamos ahora a la expresión que teníamos de la interferencia y sustituimos el espesor a por su valor:
![]()
r=0.11 cm