d =1.8·10-4 cm
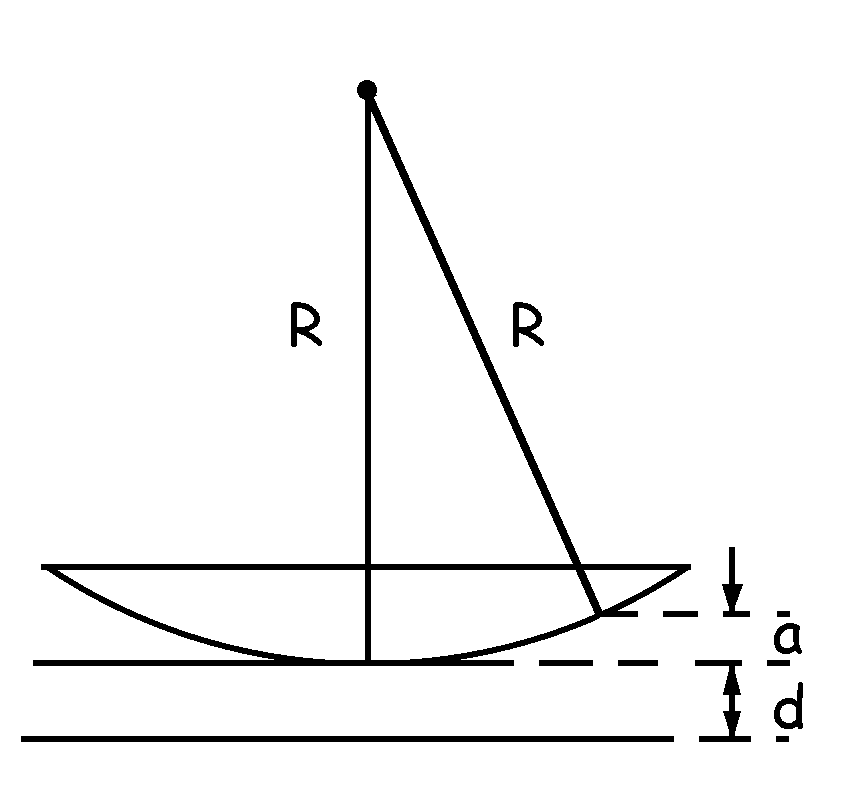 Tenemos lo que aparece en la figura, es decir, la lente flotando sobre una capa de polvo. Se producen interferencias porque entre la lente y la lámina se forma una capa de aire de espesor variable. En función del valor de este espesor tendremos que la interferencia es constructiva o destructiva, y se producen máximos y mínimos. Como el espesor es el mismo alrededor de la lente, las bandas tienen simetría circular con radio r.
Tenemos lo que aparece en la figura, es decir, la lente flotando sobre una capa de polvo. Se producen interferencias porque entre la lente y la lámina se forma una capa de aire de espesor variable. En función del valor de este espesor tendremos que la interferencia es constructiva o destructiva, y se producen máximos y mínimos. Como el espesor es el mismo alrededor de la lente, las bandas tienen simetría circular con radio r.
En el enunciado nos dicen que cuando no hay polvo, es decir, cuando la lente está directamente apoyada sobre el vidrio, el radio del quinto anillo oscuro de Newton es de 0.1 cm. Para que exista un mínimo el desfase entre las ondas debe ser igual a un número impar de veces π. En el desfase tendremos que tener en cuenta tanto la diferencia de caminos como los desfases adicionales de π radianes que producen ciertas reflexiones, en nuestro caso, la reflexión en la cara inferior de aire. Según esto la condición que tendremos es:
![]()
Suponemos que la incidencia es normal, es decir, que el ángulo de incidencia es nulo. Aplicando la ley de Snell:
nsenθi=nsenθr ⇒ nsen0º=nsenθr ⇒ 0=nsenθr ⇒ senθr=0 ⇒ θr=0º ⇒ cosθr=cos0º=1
Nos queda entonces:
![]()
La capa que produce la interferencia es de aire, luego el índice de refracción es la unidad (n=1):
2a2n=Nλ ⇒ 2a2=Nλ
Como puede verse, al aumentar N aumenta el espesor de la lámina. Cuando N=0 tendremos que el espesor a de la lámina es nulo, punto que coincide con el centro de la lente. Cuando N=1 tendremos un cierto valor de a, y por tanto de r, apareciendo el primer anillo de Newton. Para el quinto anillo:
N=5 ⇒ 2a2=Nλ ⇒ 2a2=5λ
En el problema anterior hemos visto la relación entre el espesor de la capa de aire y el radio del anillo de Newton, que es:
![]()
Sustituyendo:
![]()
Veamos qué ocurre ahora cuando existe la capa de polvo, con lo cual el radio del quinto anillo de Newton vale:
r1=0.08 cm
Al añadir la capa de polvo lo único que ocurre es que la diferencia de caminos recorrido aumenta en 2d, siendo d el espesor de la capa de polvo. La condición de mínimo y el resto serían iguales, luego llegaremos a la expresión:
2a1+2d=Nλ
La relación entre el radio del anillo y el espesor es:
![]()
Nos queda entonces:
![]()
Para el quinto anillo, igual que antes:
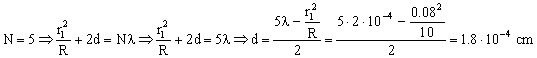
d=1.8·10-4 cm