Problema de Interferencias

Dos alambres de dos materiales distintos (1 y 2) y del mismo radio 2 mm se unen entre sí para formar un alambre más largo. En el punto de unión y en el punto más bajo del conjunto se sueldan dos anillos macizos de 250 kg de masa (ver figura). El material 1 tiene una longitud de 3 m, una densidad de 22500 kg/m3 y un módulo de Young de 8·1011 N/m2. El material 2 tiene una longitud de 7.5 m, una densidad de 2500 kg/m3 y un módulo de Young de 2·1011 N/m2. Se pide: a) calcular el alargamiento total del conjunto; b) mediante una fuente externa de frecuencia variable se producen ondas longitudinales en los dos alambres. Calcular la frecuencia más baja para la cual se producen ondas estacionarias en los alambres de modo que tanto el punto de unión como el punto más bajo sean nodos. Despreciar el alargamiento y el peso de los alambres. c) Un avión vuela horizontalmente con velocidad constante a 200 m por encima del campanario de un pueblo cuya campana emite un sonido de frecuencia 100 veces menor que la frecuencia calculada anteriormente. La velocidad del avión es 324 km/h. En un cierto instante y sobrepasado el campanario, la azafata del avión escucha el sonido de la campana con una frecuencia de 24.234 Hz. ¿Con qué frecuencia la escuchó 4.5 s antes? Velocidad del sonido en el aire: 340 m/s.

a) Δl=8.77 mm
b) ν=2981 Hz
c) ν=35.46 Hz

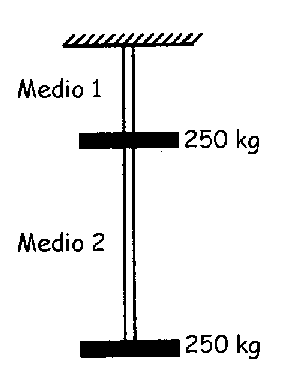
a) Supondremos que el peso de los alambres es despreciable frente al peso de los anillos. El alambre 1 por tanto, está sometido a una tensión igual al peso de los dos anillos, es decir, 500 kg. Para dicho alambre:

Haciendo lo mismo para el alambre 2 tendremos que éste está sólo sometido a una tensión igual al peso del anillo inferior, es decir, 250 kg. Por tanto:

El alargamiento total del conjunto será la suma de los alargamientos de los dos alambres:

Δl=Δl1+Δl2=1.46+7.31=8.77 mm

Δl=8.77 mm

 

b) Para que en el primer alambre se produzcan ondas estacionarias deberá cumplirse:

donde E1 es el módulo de Young, ρ1 la densidad volúmica y n1 un número entero (n1=1,2,3,…).

Haciendo exactamente lo mismo para el segundo material:

Igualando las frecuencias:

Obtenemos la ecuación:

n1=0.6n2

Sabemos que n1 y n2 son números enteros. Para obtener la frecuencia más baja que dará lugar a ondas estacionarias en los alambres tendremos que determinar los números enteros más bajos que cumplen esa ecuación. Para ello tanteamos dando valores a n2 y obteniendo los correspondientes valores de n1 hasta encontrar los dos primeros números enteros que cumplen esa relación:

n2=1 ⇒ n1=0.6n2=0.6 · 1=0.6

n2=2 ⇒ n1=0.6n2=0.6 · 2=1.2

n2=3 ⇒ n1=0.6n2=0.6 · 3=1.8

n2=4 ⇒ n1=0.6n2=0.6 · 4=2.4

n2=5 ⇒ n1=0.6n2=0.6 · 5=3.0

Ya tenemos los dos primeros enteros que cumplen esa ecuación. Sustituyendo en una cualquiera de las expresiones que nos dan la frecuencia:

ν=2981 s-1

 

c) La frecuencia de emisión será:

La velocidad del avión:

vA=324 km/h=90 m/s

Inicialmente tenemos lo que aparece en la figura. Aplicando la fórmula del efecto Doppler tendremos:

La fuente está en reposo y el observador se aleja, luego eligiendo los signos adecuados:

Sustituyendo los datos conocidos:

En el gráfico podemos ver que geométricamente:

El avión se encuentra 200 m a la derecha de la campana. En 4.5 s con movimiento rectilíneo uniforme recorre un espacio:

s=vAt=90 · 4.5=405 m

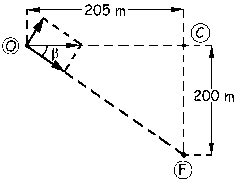Entonces tendremos que ir hacia atrás 405 m, para ver en qué posición estaba el avión 4.5 s antes. En ese momento lo tendríamos 205 m a la izquierda de la campana, es decir, como aparece en la nueva figura. El nuevo ángulo β será:

Aplicando de nuevo la ecuación del efecto Doppler:

Ahora la fuente está en reposo y el observador se acerca luego:

ν´=35.46 s-1