Problema de Interferencias

Un tubo largo está formado por la unión de dos tubos concéntricos de radios casi iguales de modo que la longitud del tubo puede variarse a voluntad. Este tubo contiene aire (masa molecular 28.84 g/mol) a 77oC. Un diapasón vibra en las proximidades de uno de sus extremos con una frecuencia de 500 ciclos/segundo. Se produce resonancia (el tubo se encuentra recorrido por ondas estacionarias) cuando la longitud del tubo se ajusta a 56.25, 93.75 y 131.25 cm, pero no para longitudes intermedias. a) Deducir con estos datos si el tubo es abierto por los dos lados, o abierto por un solo extremo; b) calcular la velocidad del sonido en aire a 77oC; c) calcular, a partir del resultado anterior, la razón ϒ de los calores específicos para el aire. d) la longitud de este tubo y de otro abierto por ambos extremos se escogen de modo que sus frecuencias fundamentales son iguales. ¿Qué otras frecuencias tienen en común ambos tubos? e) Sabiendo que la potencia sonora emitida por el tubo inicial es de 4π·10-3 W; determinar la intensidad y la sonoridad percibidas por un observador situado a 2 m del tubo sonoro. ¿A qué distancia tendrá que situarse el observador para dejar de percibir el sonido? Intensidad umbral para la frecuencia de dicho tubo: Io=4·10-12 W/m2.

a) abierto por un extremo
b) v=375 m/s
c) γ=1.39
d) 2nc+1=na
e) I=2.5·10-4 W/m2; S=77.96 dB; r=15.81 km

a) Independientemente del tipo de tubo, podemos demostrar que la diferencia entre dos longitudes sucesivas debe ser . Si el tubo fuera abierto tendríamos que para dos longitudes sucesivas del tubo:

Restando las dos longitudes:

Si el tubo fuera cerrado por un extremo tendríamos que para dos longitudes sucesivas:

Restando las longitudes:

Por tanto sin saber qué tubo tenemos, restando dos longitudes sucesivas podemos determinar la longitud de onda:

Podríamos haber elegido otro par de valores, obteniéndose el mismo resultado:

Si el tubo fuera abierto por ambos extremos se debería cumplir:

Para una de las longitudes:

Vemos que n1 no es un número entero luego el tubo no es abierto por los dos extremos. Demostraremos que sí es un tubo cerrado por un extremo. Si es cerrado por un extremo se debe cumplir que:

Para la primera de las longitudes:

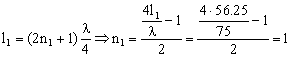
Para la segunda longitud:

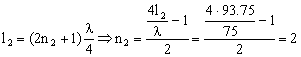
Y para la tercera de las longitudes:

Vemos que n toma valores enteros y además consecutivos. El tubo por tanto es cerrado por un extremo:

TUBO CERRADO POR UN EXTREMO

 

b) Ahora ya sabemos qué tipo de tubo es y el valor de n correspondiente a cada longitud. Utilizando una cualquiera de ellas:

v=375 m/s

Podríamos haber obtenido el mismo resultado mucho más fácilmente:

v=λν=0.75 · 500=375 m/s

c) A partir de la relación entre la velocidad y la temperatura:

ϒ=1.39

 

d) Tenemos un tubo cerrado por un extremo (al que marcaremos con el subíndice c) y otro abierto por ambos extremos (al que marcaremos con el subíndice a) para los cuales es igual la frecuencia fundamental:

Igualándolas:

Ya sabemos la relación entre las longitudes de los tubos. Vamos a ver ahora qué otras frecuencias son iguales. Para el tubo cerrado por un extremo:

Y para el tubo abierto por ambos extremos:

Igualando las frecuencias:

Dando valores a nc obtenemos los valores de na para los cuales las dos frecuencias coinciden. Podemos hacer la tabla:

nc

na

0

1

1

3

2

5

3

7

 

Coinciden todos los modos del tubo cerrado por un extremo con los modos impares del tubo abierto por ambos extremos, es decir, los valores de nc y na que cumplen la ecuación:

2nc+1=na

e) La intensidad será:

donde P es la potencia sonora y A es el área de la superficie envolvente de la onda. Como son ondas esféricas:

I=2.5 · 10-4 W/m2

La sonoridad será:

S=77.96 dB

Para que no se perciba sonido la sensación sonora debe ser nula:

Y teniendo en cuenta lo que vale la intensidad:

r=15.81 km