a) R=200.7 cm
b) d=13.42 cm
c) y´=-32.7 cm
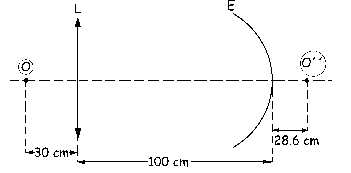
a) Tenemos el sistema que aparece en la figura. No sabemos si el espejo es cóncavo o convexo, por lo que en principio le pondremos al azar. El signo del radio nos indicará el tipo de espejo.
Conocemos el objeto O, a 30 cm de la lente, y la imagen final, O´´, que está 28.6 cm a la derecha del espejo, ya que es virtual. La focal de la lente convergente es:
![]()
En primer lugar actúa la lente convergente, para la cual el objeto es O y la imagen será O´. Para esta lente tendremos:
![]()
S´C=60 cm
La imagen O´ del objeto O está situada a la derecha de la lente convergente y a 60 cm de la misma.
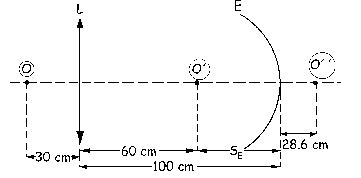
A continuación actúa el espejo, para el cual el objeto es O´ y la imagen es O´´. La distancia desde O´ hasta el espejo es:
SE=-(100-60)=-40 cm
Y ahora para el espejo:
![]()
R=200.7 cm
Como el radio del espejo es positivo significa que el espejo es convexo, y no cóncavo como le hemos dibujado hasta ahora.
b) Ahora añadimos una lente divergente entre el objeto y la convergente, cuya focal es:
![]()
La imagen final, como ahora tenemos tres elementos, será O´´´, y como es real estará situada a 10 cm del espejo y a la izquierda de él.
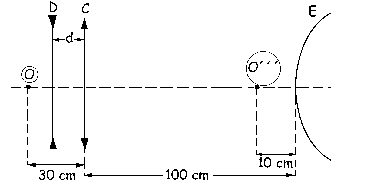
Vamos a resolver el sistema en sentido contrario. Empezaremos por el final, es decir, por el espejo, para el cual conocemos la imagen, O´´´, y el radio, pero no el objeto que sería O´´.
Para el espejo:
![]()
Esta distancia es positiva, lo que implica que el objeto O´´ está a la derecha del espejo y a 9.09 cm de él. Dicho objeto tiene que ser la imagen dada por el elemento anterior, es decir, por la lente convergente.
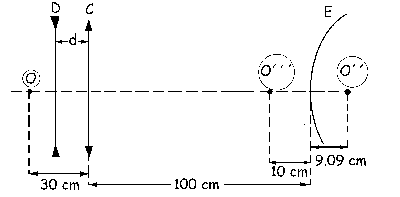
La distancia desde este punto O´´ hasta la lente convergente podemos ver en el gráfico que es:
S´C=100+9.09=109.09 cm
De modo que para la lente convergente conocemos la imagen pero no el objeto. Tendríamos:
![]()
El objeto de la lente convergente, O´, está a la izquierda de la misma (distancia negativa) y a 24.49 cm de ella. Dicho objeto debe ser la imagen de la lente divergente. Para una lente divergente el objeto y la imagen están al mismo lado de la misma, luego nos quedará el sistema tal como se muestra en la figura.
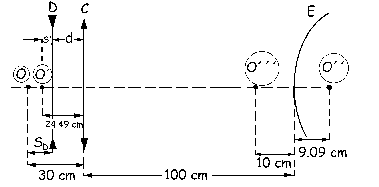
Lo primero que actuaría entonces será la lente divergente, para la cual el objeto es O y la imagen O´. Para dicha lente tendremos:
![]()
![]()
![]()
Como la lente divergente debe ir situada entre la convergente y el objeto debe cumplirse que d<30 cm, luego debemos descartar la primera solución que no se correspondería con el enunciado. Entonces:
d=13.42 cm
c) Para determinar el tamaño de la imagen tenemos que determinar el aumento lateral del sistema, que será el producto de los aumentos de los elementos que lo forman. Tendríamos entonces:
![]()
Tenemos que para la lente divergente:
SD=-(30-d)=-(30-13.42)=-15.68 cm
S´D=-(24.49-d)=-(24.49-13.42)=-11.07 cm
Nos quedará:
![]()
El aumento lateral es también la relación entre el tamaño de la imagen y el tamaño del objeto. Nos quedará por tanto:
![]()
y´=-32.7 cm