Problema de Óptica geométrica

Se dispone de una lente plano-convexa, de índice de refracción 1.5 y distancia focal 20 cm a la que se acopla otra lente de índice de refracción 1.6 de forma que las superficies en contacto tengan el mismo radio. Se desea que el sistema tenga una potencia de 8 dioptrías. a) ¿Cuál ha de ser el radio de la otra superficie de esta segunda lente? b) Se forma un sistema óptico centrado con dos lentes convergentes iguales a la anterior, es decir, de 8 dioptrías cada una. Un objeto está situado 15 cm a la izquierda de la primera lente. Calcular cuál debe ser la separación entre las dos lentes para que la imagen final sea real, derecha y cinco veces mayor que el objeto; c) entre las dos lentes convergentes se introduce una lente divergente de 20 cm de focal. Buscar las dos posiciones de esta lente para las cuales la imagen final es real y se forma a 75 cm de la última de las lentes.

a) r´=20 cm; r´=6.67 cm
b) d=100 cm
c) d1=35 cm; d2=5 cm

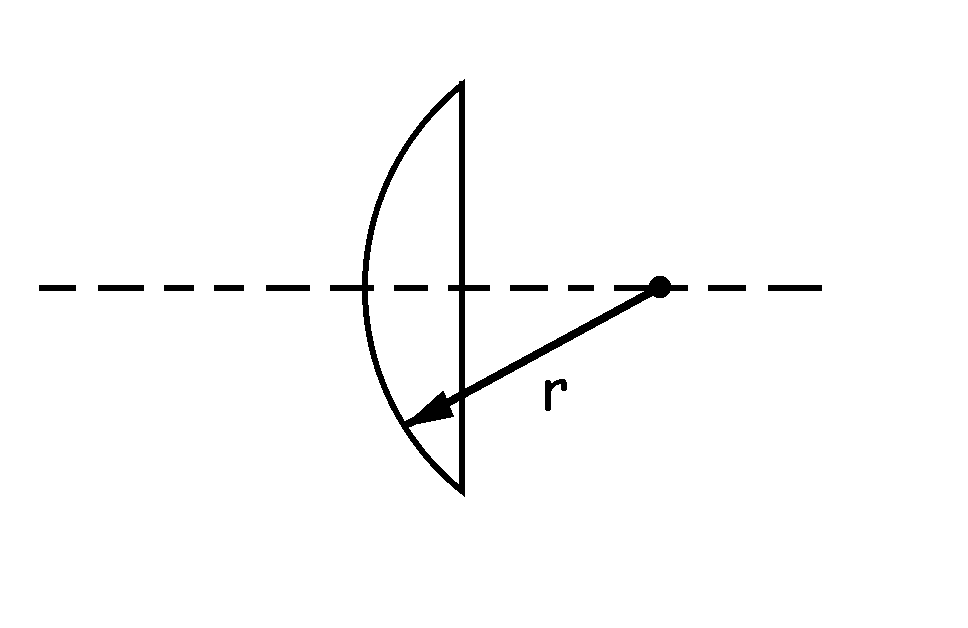a) La potencia de la lente plano-convexa, a la que llamaremos lente a, es:

El radio r de esta lente será entonces:

A esta lente se le debe acoplar otra, que llamaremos lente b, de modo que el sistema total tenga 8 dioptrías. Como son lentes yuxtapuestas las potencias son aditivas. Entonces:

P=Pa+Pb ⇒ Pb=P-Pa=8-5=3 dioptrías

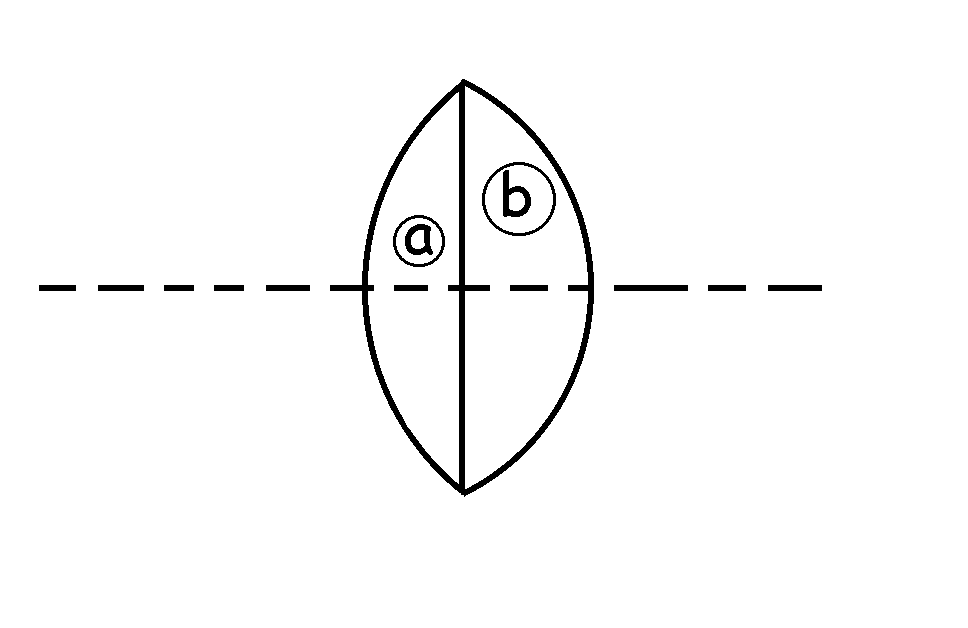Como la potencia es positiva, esto implica que la lente que hay que acoplar es también convergente. Podemos acoplarla por cualquiera de los dos lados. Se puede acoplar de manera que la cara con el radio común sea la cara plana. En este caso tendríamos:

r´=20 cm

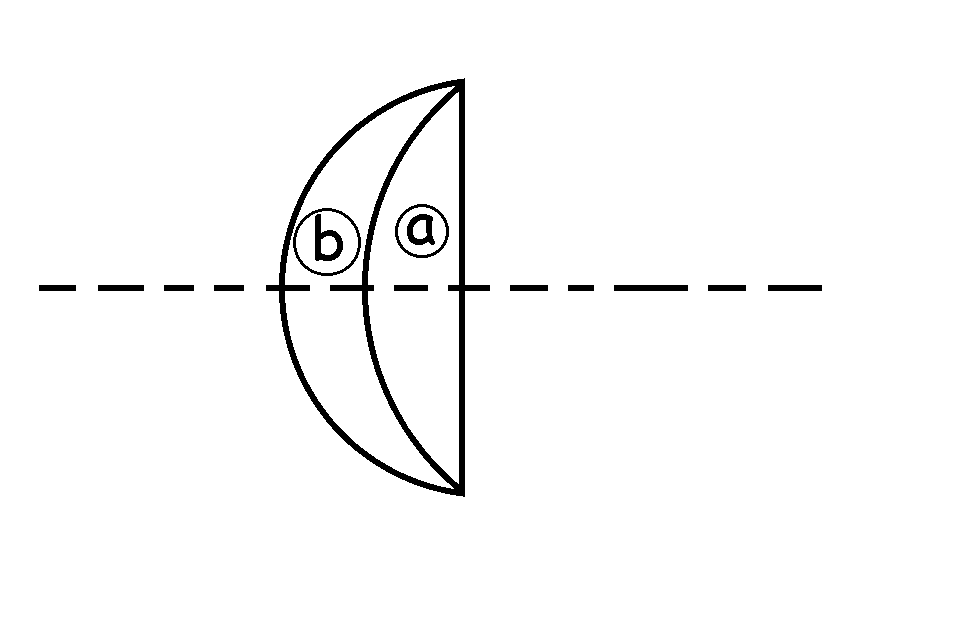También podemos acoplar la lente b de forma que la cara que tiene el radio común es la cara curva. En este segundo caso:

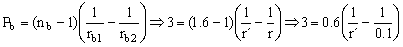
r´=0.06 m=6.67 cm

r´=6.67 cm

 

b) Ahora tenemos un sistema formado por dos lentes convergentes iguales de focales:

Actuaría en primer lugar la lente L1, para la cual el objeto O se encuentra 15 cm a su izquierda (distancia objeto negativa). Entonces:

Y el aumento de esta lente:

El aumento total del sistema es positivo ya que la imagen es derecha, y vale:

β=5

porque la imagen es cinco veces mayor que el objeto. Entonces:

Entonces tendremos que para la lente L2:

Obtenemos que para la lente L2 las distancias objeto e imagen son iguales pero de distinto signo, es decir, O´ y O´´ están a ambos lados de L2 y a la misma distancia. Tendremos lo que aparece en la figura.

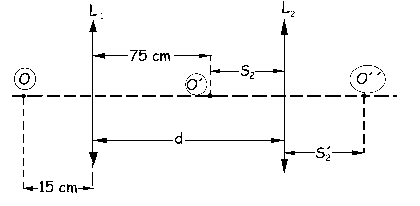
Sabemos ahora que en módulo las distancias objeto e imagen son iguales. Aplicando la ecuación de las lentes delgadas:

d-75=25 ⇒ d=75+25=100 cm

d=100 cm

 

c) Ahora tenemos una tercera lente L3 de focal:

f´3=-20 cm

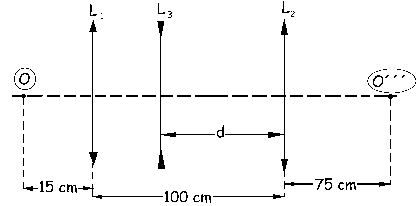
Las lentes están entonces en el orden L1→L3 →L2. Además, sabemos que la imagen final es real, luego está a la derecha de la última lente, y a 75 cm de ella. En primer lugar actúa L1, para la cual el objeto O está 15 cm a la izquierda, exactamente igual que antes.

La imagen O´ está a la derecha de L1 y a 75 cm de ella. Podemos ir también a la lente L2, que es la última. Para esta lente conocemos la imagen O´´´ pero no el objeto, luego tendremos:

El objeto O´´ de esta lente está a su izquierda y a 15 cm de ella. Tengo entonces objeto e imagen de L3 (O´ y O´´). Por ser L3 una lente divergente, el objeto y la imagen están al mismo lado de la lente. Vamos a suponer que ambos están a la derecha de L3, con lo cual tendré:

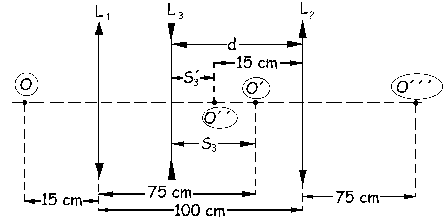
La única condición que debe cumplir d es que sea menor de 100 cm. Como los dos valores lo cumplen tenemos las dos soluciones pedidas:

d1=35 cm

d2=5 cm

Puede comprobarse que se obtiene exactamente la misma solución si se supone al llegar a la lente divergente que tanto O´ como O´´ están a la izquierda de L3.