a) P= 10 dioptrías
b) r1=15 cm; r2=7.5 cm; r1=2.5 cm; r2=5 cm
c) n´=1.5
a) La imagen es real y la lente convergente. Esto significa que el objeto está situado a la izquierda de la lente (distancia objeto negativa) mientras que la imagen se forma a la derecha de ella (distancia imagen positiva). El aumento lateral de la lente valdrá:
Como el objeto está situado a 15 cm de la lente:
S=-15 cm ⇒ S´=-2S=-2 · (-15)=30 cm
Aplicando la ecuación de las lentes delgadas:
Y la potencia en dioptrías es el inverso de la distancia focal en metros:
P=10 dioptrías
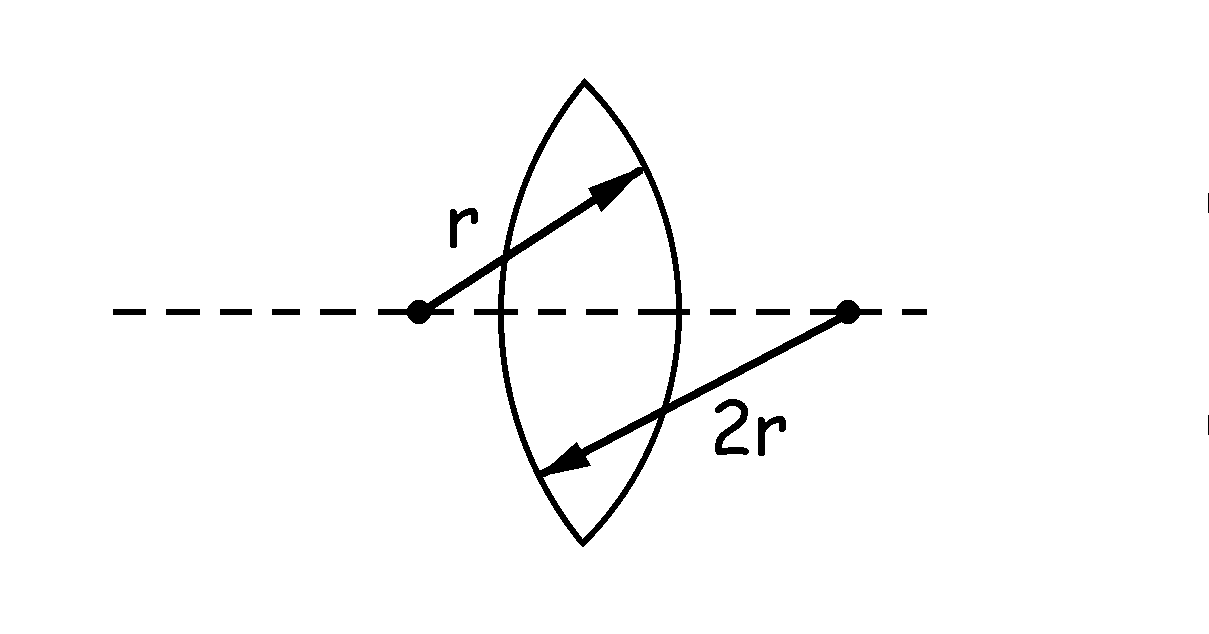b) Podemos tener dos posibilidades para que la lente sea convergente y sus radios de curvatura estén en la relación 1 a 2. La primera de ella es que la lente sea biconvexa, en cuyo caso:
Los radios de curvatura en este caso son:
r1=2r=2 · 7.5=15 cm
r1=15 cm
Y el de la otra cara:
r2=r=7.5 cm
r2=7.5 cm
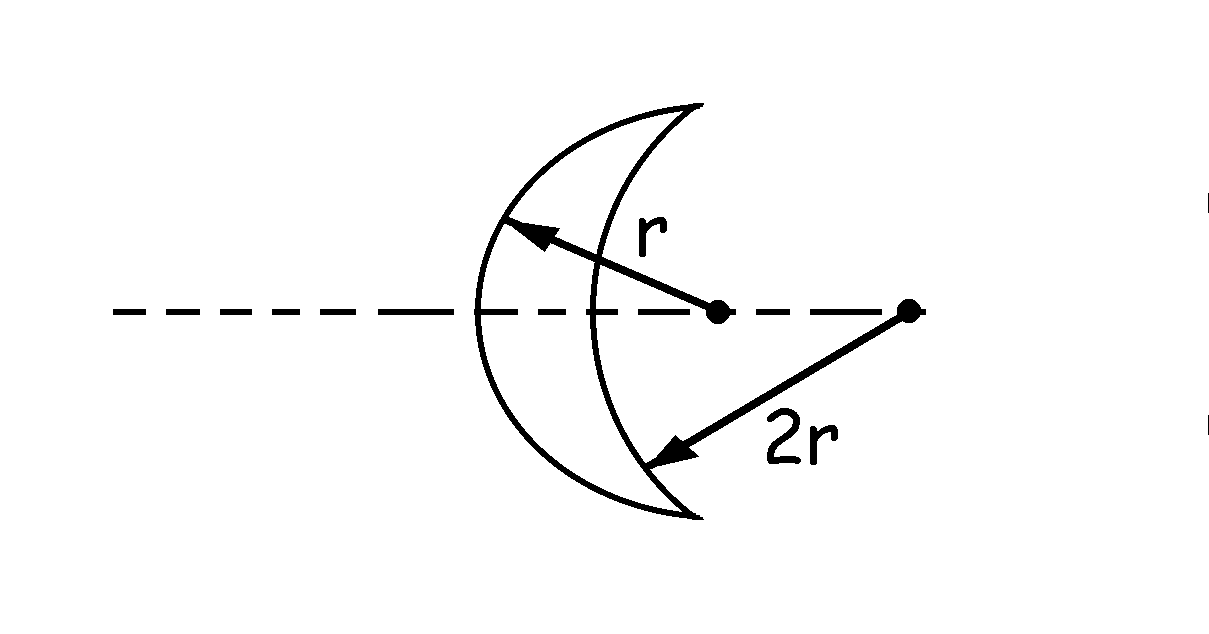Y la otra posibilidad es que la lente sea convexo-cóncava. En este segundo caso tendremos:
El radio de curvatura de la cara 1 es entonces:
r1=r=2.5 cm
r1=2.5 cm
Y el de la cara 2:
r2=2r1=2 · 2.5=5 cm
r2=5 cm
c) Al introducir la lámina de vidrio, la imagen se forma 20 cm más lejos que antes. Si antes la imagen estaba a 30 cm, ahora estará a 50 cm y a la derecha de la lente por ser real. Actuarán de modo consecutivo la primera cara de la lámina, la segunda cara de la lámina y la lente convergente, de manera que la imagen final será O´´´. Tendremos el sistema inicial que aparece en la figura, donde llamaremos n´ al índice de refracción de la lámina y na al del aire, que vale la unidad.
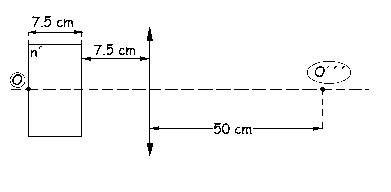
Para la primera cara de la lámina de vidrio aplicamos el invariante de Abbe, teniendo en cuenta que el radio de curvatura de las caras es infinito, y que la distancia desde el objeto O hasta la primera cara de la lente es nula:
La imagen O´ dada por la primera cara de la lente coincide con esta cara, y por tanto con el objeto O.
Vamos ahora a la lente, para la cual tenemos la imagen O´´´, pero no el objeto O´´.
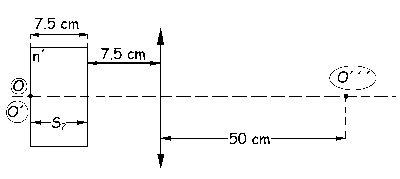
Para la lente convergente:
El objeto de la lente, que es O´´ se forma a su izquierda y a 12.5 cm de la lente. Ahora ya tenemos para la segunda cara de la lámina de vidrio el objeto y la imagen, que serán respectivamente O´ y O´´.
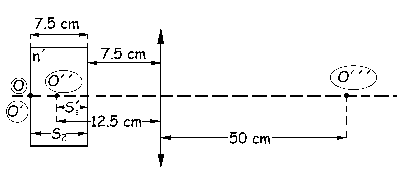
Aplicamos el invariante de Abbe a esta segunda cara de la lámina, para la cual:
S2=-7.5 cm; S´2=-(12.5-7.5)=-5 cm
Para esta cara:
n´=1.5