a) f´=24.50 cm
b) d=99 cm
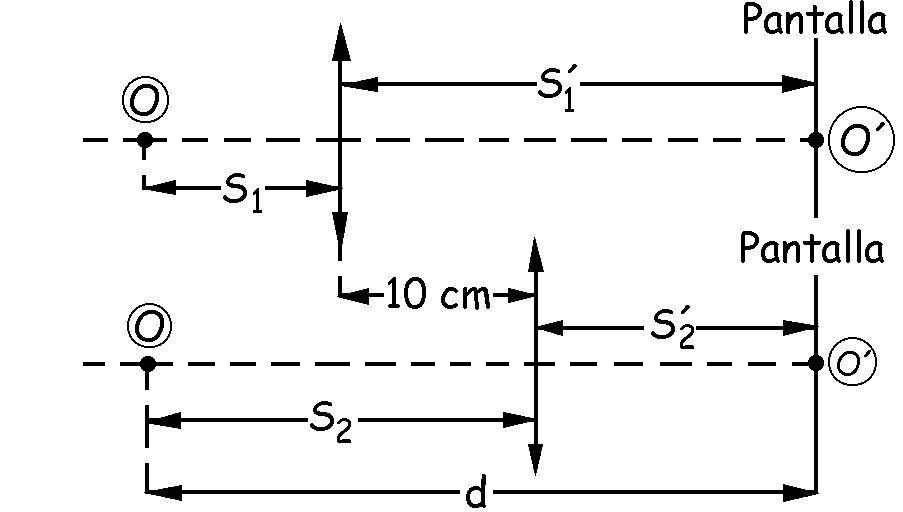a) Tendremos dos situaciones en las que se mantiene la distancia entre el objeto y la imagen (d) y para las cuales las posiciones de la lente están separadas por 10 cm. La imagen se proyecta sobre una pantalla, de modo que es real. Por tanto en ambas situaciones el objeto está a la izquierda de la lente (distancia objeto negativa) y la imagen a la derecha de la misma (distancia imagen positiva). En cada uno de los casos el tamaño de la imagen será, teniendo en cuenta el signo de las distancias y que el objeto es el mismo en los dos casos:
El cociente entre los tamaños en los dos casos es 
luego:
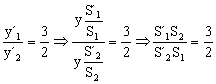
Como ya hemos tenido en cuenta los signos en las distancias obtendremos como resultados valores absolutos. En ambos casos la distancia focal es la misma, ya que la lente no ha cambiado, luego:
Los primeros miembros son iguales luego los segundos también lo serán:
En los dos casos la distancia entre el objeto y la pantalla es:
d=S1+S´1=S2+S´2
Teniendo en cuenta esto la ecuación anterior nos queda:
Además, podemos ver en el gráfico que:
S2-S1=10 cm
S´1-S´2=10 cm
Por tanto, recopilando, tenemos un sistema de cuatro ecuaciones y cuatro incógnitas:
S1S´1=S2S´2
S2-S1=10
S´1-S´2=10
De la tercera ecuación:
S2-S1=10 ⇒ S2=10+S1
Sustituimos en las otras tres y nos quedan:
S1S´1=S2S´2 ⇒ S1S´1=(10+S1)S´2
S´1-S´2=10
De esta última ecuación:
S´1-S´2=10 ⇒ S´1=10+S´2
Y sustituimos en las otras dos:
S1S´1=(10+S1)S´2 ⇒ S1(10+S´2)=(10+S1)S´2
Ahora de la segunda ecuación:
S1(10+S´2)=(10+S1)S´2 ⇒ 10S1+S1S´2=10S´2+S1S´2
10S1=10S´2 ⇒ S1=S´2
Sustituimos esto en la primera ecuación que nos quedaba:
Descartamos la solución negativa, ya que hemos tenido en cuenta todos los signos y por tanto sólo debemos obtener valores absolutos. Entonces:
S1=44.49 cm
Vamos determinando ahora los demás parámetros:
S´2=S1=44.49 cm
S´1=10+S´2=10+44.49=54.49 cm
S210+S1=10+44.49=54.49 cm
Y por último la focal:
f´=24.50 cm
b) Y la distancia entre la pantalla y el objeto:
d=S1+S´1=44.49+54.49=99 cm
d=99 cm