a) rb1=24 cm; rb2=48 cm; ó rb1=39 cm; rb2=78 cm
b) s´c=72 cm; imagen: real, invertida y menor
c) d=196 cm; R=86.4 cm.
 a) La lente divergente puede ser en primer lugar como aparece en la figura, siendo:
a) La lente divergente puede ser en primer lugar como aparece en la figura, siendo:
na=1.5; nb=1.6
Como la potencia de las lentes yuxtapuestas es aditiva:
![]()
![]()
![]()
Entonces el primer radio de la lente bicóncava es:
rb1=r=24 cm
rb1=24 cm
Y el segundo:
rb2=2r=2 · 24=48 cm
rb2=48 cm
 Existe otra posibilidad, que es que los radios en vez de ser r y 2r, fueran al contrario, 2r y r. Tendríamos entonces lo que aparece en la figura. En este segundo caso, haciendo lo mismo que antes:
Existe otra posibilidad, que es que los radios en vez de ser r y 2r, fueran al contrario, 2r y r. Tendríamos entonces lo que aparece en la figura. En este segundo caso, haciendo lo mismo que antes:
![]()
![]()
![]()
Entonces el primer radio de la lente bicóncava es:
rb1=r=39 cm
rb1=39 cm
Y el segundo:
rb2=2r=2 · 39=78 cm
rb2=78 cm
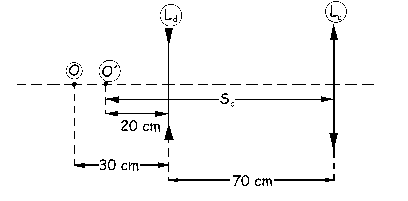
b) Ahora tendremos el sistema óptico que aparece en la figura.

En primer lugar actúa la lente divergente, para la cual el objeto es O y la imagen O´. Para esta lente:
![]()
![]()
La imagen O´ se forma a la izquierda de la lente divergente y a 20 cm de ella. Dicha imagen es el objeto para el elemento siguiente, es decir, para la lente convergente. Para esta lente el objeto es O´ y la imagen es O´´.
Tendremos que:
Sc=-(70+20)=-90 cm
Aplicando la ecuación de las lentes delgadas:
![]()
S´c=72 cm
La imagen final se forma a la derecha de la lente convergente y a 72 cm de ella. Como se forma por los propios rayos la imagen es real.
En cuanto al aumento lateral, el aumento lateral del sistema será el producto de los aumentos laterales de los elementos que lo componen, es decir:
![]()
El aumento lateral es negativo luego la imagen está invertida respecto del objeto. Además, como en módulo es menor que la unidad la imagen es menor que el objeto.
IMAGEN REAL, INVERTIDA Y MENOR
c) Tenemos ahora el sistema que aparece en la figura.
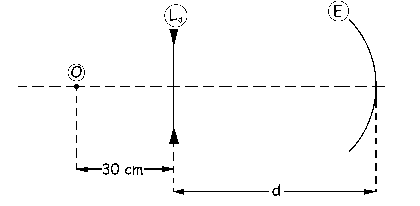
En primer lugar actúa la lente divergente, para la cual el objeto es O y la imagen O´. Para esta lente:
![]()
![]()
La imagen intermedia O´ se forma a la izquierda de la lente divergente y a 20 cm de ella. Para esta lente el aumento lateral será:
![]()
También conocemos la distancia entre el objeto O y la imagen final O´´ ya que nos dicen que debe ser la misma que en el apartado anterior:
OO´´=72+70+30=172 cm
Además, como la imagen O´´ es real debe estar situada a la izquierda del espejo. Por tanto, para el espejo, tanto el objeto (O´) como la imagen (O´´) están a la izquierda. Podemos determinar el aumento del espejo, ya que sabemos que la imagen final es 6 veces menor que el objeto:
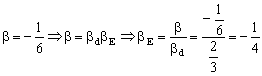
Además, en módulo:
![]()
Gráficamente tendremos lo que aparece en la figura:
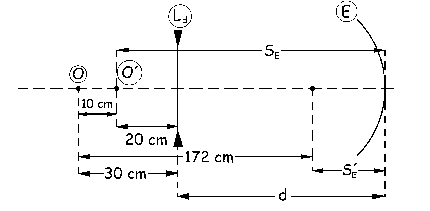
Teniendo en cuenta todo lo que hemos explicado. Podemos escribir:
|SE|=4|S´E|
|SE|=172+|S´E|-10 ⇒ |SE|=162+|S´E|-10
Resolviendo el sistema de ecuaciones:
|S´E|=54 cm
Y la distancia objeto:
|SE|=216 cm
La distancia entonces entre la lente y el espejo es:
d=|S’E|+172-30=54+172-30=196 cm
d=196 cm
Y a través de la ecuación del espejo determinamos su radio:
![]()
R=86.4 cm