a) R=20 cm
b) d=53.33 cm
c) d=26.65 cm
d) Caso a: β=2, Imagen virtual, derecha y mayor que el objeto; Caso b: β=-6, Imagen real, invertida y mayor que el objeto. Caso c: β=-3.6, Imagen real, invertida y mayor que el objeto.
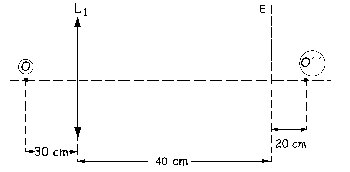
a) Tenemos el sistema que aparece en la figura. No sabemos si el espejo es cóncavo o convexo. El signo del radio nos indicará el tipo de espejo.
Conocemos el objeto O, a 30 cm de la lente, y la imagen final, O´´, que está 20 cm a la derecha del espejo, ya que es virtual. La focal de la lente convergente es:
En primer lugar actúa la lente convergente, para la cual el objeto es O y la imagen será O´. Para esta lente tendremos:
s´C=60 cm
La imagen O´ del objeto O está situada a la derecha de la lente convergente y a 60 cm de la misma.
A continuación actúa el espejo, para el cual el objeto es O´ y la imagen es O´´. La distancia desde O´ hasta el espejo es:
SE=-(40-60)=20 cm
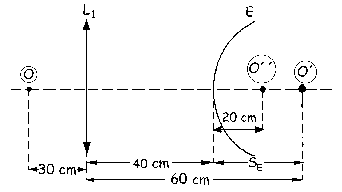
Y ahora para el espejo:
R=20 cm
Como el radio del espejo es positivo significa que el espejo es convexo.
b)Si queremos que la imagen dada por el sistema sea real y esté a 20 cm del espejo tenemos que variar la distancia entre la lente L1 y el espejo; si denominamos d a dicha distancia, tenemos:
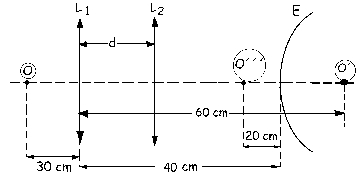
c) Ahora añadimos otra lente convergente de 2 dioptrías entre la lente y el espejo que teníamos,inicialmente, para que la imagen final sea real y esté a 20 cm del espejo.
La focal de esta nueva lente es:
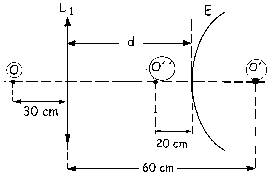La imagen final, como ahora tenemos tres elementos, será O´´´, y como es real estará situada a 20 cm del espejo y a la izquierda de él. Vamos a resolver el sistema en sentido contrario. Empezaremos por el final, es decir, por el espejo, para el cual conocemos la imagen, O´´´, y el radio, pero no el objeto que sería O´´.
Para el espejo:
Esta distancia es positiva, lo que implica que el objeto O´´ está a la derecha del espejo y a 6.66 cm de él. Dicho objeto tiene que ser la imagen dada por el elemento anterior, es decir, por la lente convergente intercalada. La distancia desde este punto O´´ hasta dicha lente es:
s´C=40+6.66-d=(46.66-d) cm
Ese punto O´´ es la imagen del punto O´ que esta situado de la lente L1 a 60 cm a su derecha, como habíamos calculado en el apartado a). De modo que ahora tendremos para la lente L2:
La distancia a la que tendríamos que colocar la lente L2 de la L1 es d=26.65 cm; ya que el otro valor de d, d=80 cm implica que tendríamos que colocar la lente L2 a la derecha del espejo y por tanto no actuaría ésta
d) Respecto al carácter de la imagen en el caso a) es virtual.
El aumento vale:
β=βL1×βE’=
Por lo que la imagen es mayor y derecha
En el caso b), la imagen es real. El aumento:
β’=βL1×βE’=
por lo que la imagen es invertida y mayor que el objeto
En el caso c) es real ; el aumento:
β»=βL1×βL2×βE’=
luego la imagen es invertida y mayor que el objeto pero menor que la obtenida en el apartado anterior.