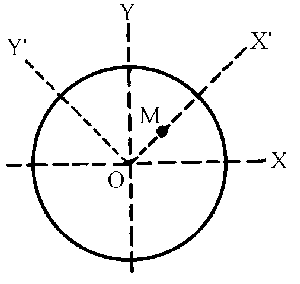aMX´=10.97 m/s2; aMY´=4.374 m/s2
Tomaremos como sistema de referencia unos ejes X´Y´ tales como los que aparecen en el gráfico, con el eje Z´ perpendicular a X´ y a Y´ y positivo saliendo hacia fuera. Denominaremos i´, j´ y k´ a los vectores unitarios en este sistema. De este modo, las dos componentes que obtengamos de la aceleración absoluta estarán ya en las direcciones que buscamos y no habrá que realizar ninguna proyección.
La aceleración absoluta del punto M es:
aM=aO+α X OM-ω2OM+2ω X vr+ar
Vamos a ir determinando cada uno de estos términos. El punto O es un punto fijo, luego no tiene ni velocidad ni aceleración:
aO=0
El movimiento de rotación es uniformemente acelerado, luego la aceleración angular tienen el mismo sentido que la velocidad angular, es decir, horario. Vectorialmente será entonces:
α=-k
El vector de posición OM en el tiempo t=5/3 es:
![]()
Vectorialmente:
OM=-0.866i´
Para la velocidad angular tendremos en cuenta que el movimiento de rotación es uniformemente acelerado y que además se parte del reposo, luego:
![]()
Vectorialmente, como tiene sentido horario:
ω=-1.67k´
La velocidad relativa será la derivada respecto del tiempo del vector de posición relativo. Si nos situamos en el disco, el vector de posición que veríamos sería x´, y el movimiento sólo se produciría a lo largo de este diámetro, por lo que:
![]()
Para t=5/3 s:
![]()
Como el movimiento sólo existiría en el eje X´:
vr=1.57i´
Y la aceleración relativa será la derivada de la velocidad relativa respecto del tiempo:
![]()
Cuando t=5/3 s:
![]()
Y vectorialmente:
ar=8.55i´
Sustituyendo todo tendremos:
aM=aO+α X OM-ω2OM+2ω X vr+ar=
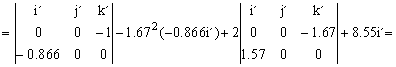
=0.866j´+2.42i´-5.24j´+8.55i´=10.97i´-4.374j´
Esto será directamente la proyección sobre los ejes que nos interesan, luego:
aMX´=10.97 m/s2
aMY´=4.374 m/s2