a) F=0.197 N; Ec=0.0395 J; Lo=0.025 kg m2/s
b) W=0.592 J; La energía cinética final es 16 veces superior a la energía cinética inicial
a) En primer lugar vamos a expresar todas las magnitudes físicas que son datos del problema en unidades del Sistema Internacional:
m=50 g=0.050 kg; r=40 cm=0.40 m
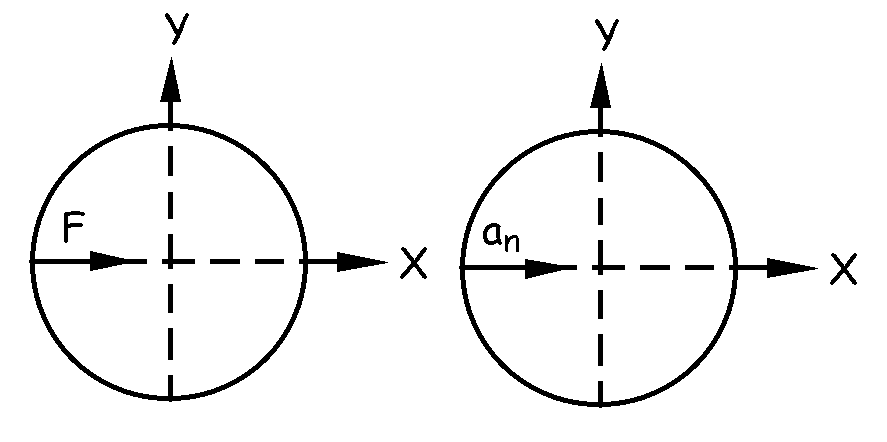Aislamos la partícula y representamos su diagrama de sólido libre. Aplicando la segunda ley de Newton y teniendo en cuenta que el movimiento que está realizando es un movimiento circular uniforme con velocidad angular ω
y radio de curvatura r tenemos:
F=man=mω2r=0.05 · π2 · 0.40=0.197 N
F=0.197 N
La energía cinética de la partícula será:
EC=0.0395 J
El momento angular respecto de O, LO, es el momento del vector mv (cantidad de movimiento de la partícula) respecto del punto O. Viene dado por tanto por la expresión:
LO=r X mv
El momento angular es un vector perpendicular a r y a mv, cuyo módulo es el producto de los módulos de ambos vectores por el seno del ángulo que forman:
LO=rmvsen90º=rmv
ya que por ser la velocidad tangente a la trayectoria estos dos vectores son perpendiculares. Sustituyendo por los respectivos valores:
LO=rmv=rmω
r=mω
r2=0.05 · π· 0.402=0.025 kgm2/s
LO=0.025 kgm2/s
b) El trabajo realizado por la persona que tiró de la cuerda es igual a la variación de energía cinética de la partícula entre la situación inicial, cuando describía una circunferencia de radio r=0.40 m y centro O, con una velocidad angular de ω=30 r. p. m. y la situación final donde describe una circunferencia de radio 
con una velocidad angular ω’ que tendremos que determinar. El trabajo por tanto es:
Como la fuerza que actúa en todo momento sobre la partícula es una fuerza central que pasa por O, el momento de la fuerza respecto a dicho punto O es nulo; por tanto se conserva el momento angular de la partícula con respecto a dicho punto:
Sustituyendo por tanto el trabajo será:
W=0.592 J
No se conserva la energía cinética de la partícula:
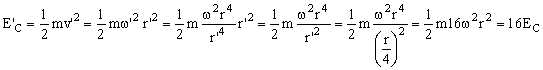
La energía cinética final es 16 veces superior a la energía cinética inicial.