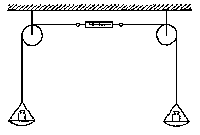
F=30 N; ΔP=30 N

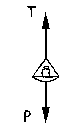El sistema estará en equilibrio, luego el dinamómetro marcará el valor de la tensión de la cuerda de uno cualquiera de los lados (obviamente el otro lado del dinamómetro actúa sólo como sujeción). En este primer caso entonces el dinamómetro marca la tensión de la cuerda. El sistema está en equilibrio, luego para uno cualquiera de los platos, como aparece en la figura tendremos:

ΣF=0 ⇒ T-P=0 ⇒ T=P=30 N

F=30 N

El peso de 30 N es igual a una masa de:

Y los 10 N que quitamos son una masa de:

En este segundo supuesto, el sistema, al quitar de uno de los platos un peso de 10 N tenderá a moverse con movimiento uniformemente acelerado, pero la tensión en la cuerda, que es lo que marca el dinamómetro, debe seguir siendo 30 N. Además, la aceleración de los dos platos será la misma. Supongamos que quitamos 10 N del plato de la izquierda y añadimos P al de la derecha. En el plato de la izquierda nos quedará una masa m₁ de:

m₁=3.06-1.02=2.04 kg

Y en el de la derecha nos quedará una masa de:

m₂=3.06+Δm

siendo Δm la masa que hay que añadir en el platillo de la derecha.

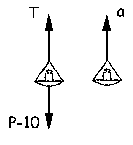En el plato de la izquierda tendremos, de acuerdo a lo que muestra en la figura:

ΣF=m₁a ⇒ T-P+10=m₁a ⇒ T-30+10=2.04a ⇒ T-20=2.04a

En el platillo de la izquierda tendremos lo que aparece en esta segunda figura. Se cumplirá que:

ΣF=m₂a ⇒ P+Δmg-T=(3.06+Δm)a ⇒ 30+Δmg-T==(3.06+Δm)a

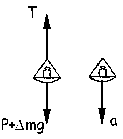En las dos ecuaciones podemos despejar la aceleración, que es la misma en los dos casos, y nos quedará:

Igualando las dos expresiones:

Y teniendo en cuenta que el dinamómetro (que nos da la tensión) debe seguir marcando 30 N:

Y el peso será:

ΔP=Δmg=3.06 · 9.8=30 N

ΔP=30 N