T máxima: punto más bajo de la trayectoria; T mínima: extremo de la oscilación

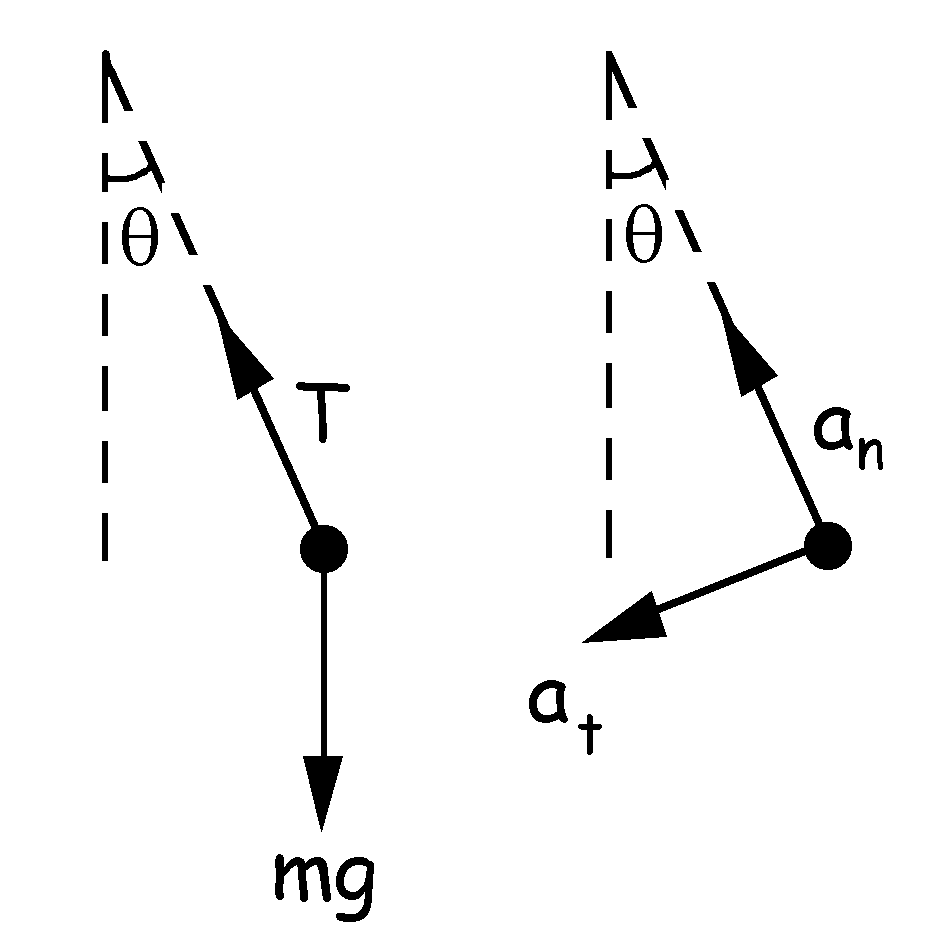Tomaremos como sistema de ejes el de la dirección normal y el tangencial. En un punto cualquiera de la trayectoria de la partícula el sistema de fuerzas que actúan sobre ella es el que aparece en la figura, siendo θ el ángulo que en ese momento forma la cuerda con la vertical. En cuanto a aceleraciones estará sometida a la aceleración normal en la dirección del radio de curvatura y apuntando hacia el centro de curvatura y a la aceleración tangencial en dirección perpendicular a la anterior. En la dirección normal aplicando la segunda ley de Newton tendremos:

En esta ecuación tenemos dos variables, v y cosθ . La tensión del hilo será máxima cuando estas dos variables sean máximas, es decir, en el punto más bajo de la trayectoria, en el cual la velocidad es máxima y el ángulo θ es nulo, con lo cual el coseno adquiere también su valor máximo:

θ=0 ⇒ cosθ=1

T máxima ⇒ punto más bajo de la trayectoria

Por el contrario, la tensión será mínima cuando esas dos variables tomen el valor mínimo. Esto se producirá en el extremo de la oscilación, donde la velocidad es nula y el cosq
toma el valor mínimo.

T mínima ⇒extremo de la oscilación