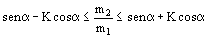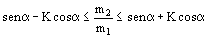
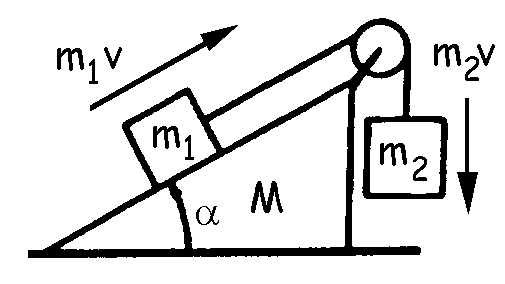
Para todo el sistema no existen fuerzas externas en el eje X, ya que las únicas fuerzas que actuarían sobre el sistema total serían los pesos y la normal ejercida por el suelo sobre la cuña, todas ellas verticales (eje Y). Esto implica que el el eje X la cantidad de movimiento del sistema debe conservarse, y además, debe ser nula, ya que el sistema parte del reposo.

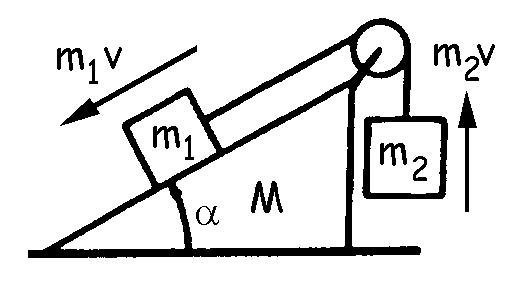Esto quiere decir que si m₁ se moviera hacia arriba y m₂ hacia abajo, la cuña debería moverse hacia la izquierda para anular la componente en X de m₁v. Lo mismo ocurre si suponemos que m₁ baja y m₂ sube. Para que en el eje X se anule la cantidad de movimiento la cuña debería moverse hacia la derecha y contrarrestar la componente en X de m₁v. Como la cuña no debe moverse, tampoco deberán moverse ni m₁ ni m₂. Por tanto la condición del problema será el equilibrio de todas las partes del sistema.

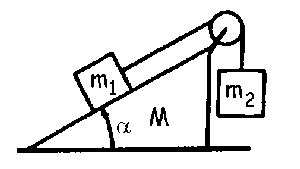
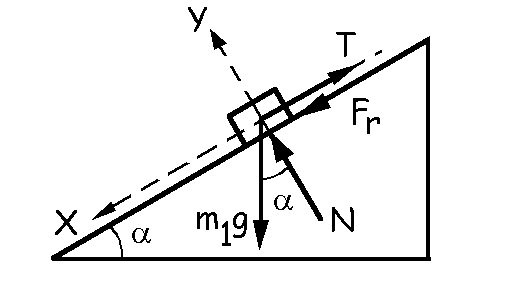El valor límite por uno de los extremos implicará que m₁ esté a punto de deslizar hacia arriba, con lo cual tendremos lo que aparece en la figura. Como el sistema está en reposo:

ΣF_Y=0 ⇒ N-m₁gcosα=0 ⇒ N=m₁gcosα

ΣF_X=0 ⇒ m₁gsenα+F_r-T=0 ⇒ F_r=T-m₁gsena

Como el bloque no debe deslizar:

F_r ≤ (F_r)_máx ⇒ F_r≤ KN ⇒ T-m₁gsenα ≤ Km₁gcosα ⇒ T ≤ m₁gsenα+Km₁gcosα

Si además aislamos la masa m₂ tendremos que como debe estar en equilibrio:

ΣF_Y=0 ⇒ -m₂g=0 ⇒T=m₂g

Sustituyendo esta expresión de la tensión en la obtenida a partir del aislamiento de m₁ tenemos:

m₂g ≤ m₁gsenα+Km₁gcosα

Y dividiendo por m₁ nos queda la relación de masas:

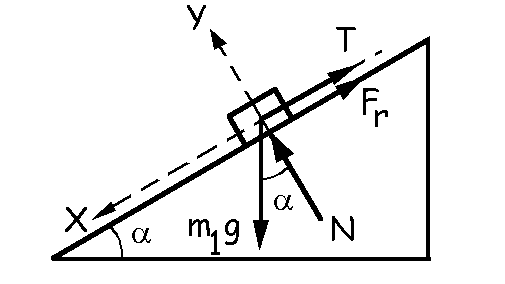Veamos ahora qué ocurre si m₁ está a punto de deslizar hacia abajo. En este caso el diagrama de sólido libre de m₁ será distinto ya que la fuerza de rozamiento tendrá sentido contrario al anterior. Aplicando las condiciones de equilibrio:

ΣF_Y=0 ⇒N-m₁gcosα=0 ⇒ N=m₁gcosa

ΣF_X=0 ⇒ m₁gsenα-F_r-T=0 ⇒ F_r=m₁gsenα-T

Igual que antes, como m₁ no debe deslizar se cumplirá que:

F_r ≤ (F_r)_máx ⇒ F_r ≤ KN ⇒ m₁gsenα-T≤ Km₁gcosα ⇒T≤ m₁gsenα-Km₁gcosα

Para la masa m₂ tenemos el mismo diagrama que antes, luego haciendo lo mismo:

ΣF_Y=0 ⇒ T-m₂g=0 ⇒ T=m₂g

Sustituyendo el valor de T obtenido en esta expresión en la anterior:

m₂g ≤ m₁gsenα-Km₁gcosα

Y dividiendo por m₁ obtenemos la relación de masas:

Tenemos por tanto, reuniendo las dos situaciones, las condiciones:

Estas dos condiciones se pueden englobar en una sola que será: