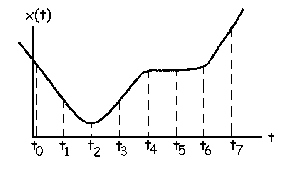
a) to y t1
b) t3, t4, t6 y t7
c) t2 y t5
d) t4
e) t2 y t6
f) to, t1, t3, t5 y t7
a) La velocidad es la derivada del espacio respecto del tiempo, es decir:
![]()
Geométricamente esto es la pendiente de la tangente en el punto dado. Por tanto, la velocidad será negativa cuando la pendiente en ese punto sea negativa, es decir, en t0 y t1.
t0 y t1
b) La velocidad será positiva en los puntos en los cuales la pendiente de la tangente sea positiva, es decir, en t3, t4, t6 y t7.
t3 t4, t6 y t7
c) La velocidad será nula cuando lo sea la pendiente de la tangente, o sea, cuando la tangente sea horizontal a la curva. Esto sucede en los puntos t2 y t5.
t2 y t5
d) En t4 la velocidad pasa de ser positiva (pendiente de la tangente positiva un instante antes) a ser nula (tangente horizontal y por tanto pendiente de la tangente nula un instante después), luego para que la velocidad disminuya la aceleración debe ser negativa.
t4
e) En t2 la velocidad pasa de ser negativa a positiva, es decir, aumenta, luego la aceleración debe ser positiva. En t6 la velocidad pasa de ser nula a positiva, luego también aumenta y la aceleración será positiva.
t2 y t6
f) Como el movimiento es unidimensional, la aceleración será nula cuando la velocidad sea constante, es decir, en los intervalos en que la gráfica espacio-tiempo sea recta. Esto sucede en los puntos t0, t1, t3, t5 y t7.
t0, t1, t3, t5 y t7