Problema de Entropia y Segundo Principio de la Termodinámica

Un gas perfecto que se encuentra a 27 oC ocupa un volumen de 4.1 l, estando sometido a una presión de 12 atm. A partir de este estado sufre las siguientes transformaciones reversibles: 1) se calienta a volumen constante hasta que la presión se duplica; 2) a continuación se expande isotérmicamente hasta que recupera la presión inicial; 3) finalmente se comprime a presión constante hasta que recupera el estado inicial. Se pide: a) dibujar el proceso en un diagrama P-V; b) calcular los calores y trabajos intercambiados por el gas en cada uno de los procesos, así como la variación de energía interna para cada uno de ellos; c) lo mismo que en b) para todo el ciclo.
Datos: cv=5 cal/mol; R=0.082 atm·l/molK=8.32 J/molK=2 cal/molK; 1 atm=101324.72 N/m2.

a)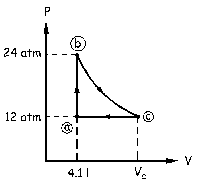
b) ΔQab=3000 cal; ΔWab=0; ΔUab=3000 cal; ΔUbc=0; ΔWbc=1653.33 cal; ΔQbc=1653.33 cal; ΔQca=-4200 cal; ΔWca=-1192.63 cal; ΔUca=-3007.37 cal
c) ΔU=0; ΔQ=453.33 cal; ΔW=460.07 cal

a) El ciclo se inicia en el punto que denominaremos a. En este punto conocemos la presión, 12 atm, y el volumen, 4.1 l. Desde aquí se calienta el gas a volumen constante, es decir, tendremos que dibujar una recta paralela al eje de presiones hasta el punto b, en el cual el volumen es el mismo que en a, y la presión el doble:

Pb=2Pa=2 · 12=24 atm

Después se expande el gas isotérmicamente, luego dibujaremos una línea curva hasta el punto c, en el cual la presión es la misma que la inicial, es decir, 12 atm, y el volumen es desconocido.

Por último se realiza una compresión a presión constante, luego dibujaremos una recta paralela al eje de volúmenes hasta las condiciones iniciales, es decir, de nuevo hasta el punto a. Tendremos pues el gráfico de la figura.

b) Determinaremos en primer lugar el calor específico a presión constante, teniendo en cuenta que:

cP=cV+R=5+2=7 cal/molK

La transformación a — b es a volumen constante luego el calor intercambiado es:

ΔQab=ncVΔTab=ncV(Tb-Ta)

El número de moles podemos calcularlo aplicando la ecuación de los gases perfectos al estado a, sabiendo que la temperatura en este punto es:

Ta=27ºC=300 K

Entonces:

Ahora nos falta la temperatura en el punto b. Como la transformación es a volumen constante se cumplirá que:

El calor intercambiado en esta transformación es pues:

ΔQab=ncV(Tb-Ta)=2·5(600-300)=3000 cal

ΔQab=3000 cal

Por ser a volumen constante el trabajo realizado es nulo:

ΔWab=0

Y la variación de energía interna la determinamos por el primer principio de la Termodinámica:

ΔQab=ΔWab+ΔUab ⇒ ΔUab=ΔQab-ΔWab=ΔQab=3000 cal

ΔUab=3000 cal

La transformación b — c es isoterma luego la variación de energía interna es nula:

ΔUbc=0

El trabajo realizado es:

Por la ecuación de los gases perfectos:

PbVb=nRTb

Luego nos queda:

Y nos falta determinar el volumen en el punto c. Como la transformación es isoterma se cumple:

El trabajo entonces en esta transformación es:

ΔWbc=1653.33 cal

Y la variación de calor la determinamos a través del primer principio de la Termodinámica:

ΔQbc=ΔUbc+ΔWbc=ΔWbc=1653.33 cal

ΔQbc=1653.33 cal

La transformación c — a es isobara (a presión constante) luego el calor intercambiado es:

ΔQca=ncPΔTca=ncP(Ta-Tc)=2 · 7(300-600)=-4200 cal

ΔQca=-4200 cal

El trabajo realizado:

ΔWca=PaΔVca=Pa(Va-Vc)=12(4.1-8.2)=-49.2 atm · l=

ΔWca=-1192.63 cal

Y por el primer principio de la Termodinámica:

ΔQca=ΔUca+ΔWca ⇒ ΔUca=ΔQca-ΔWca=-4200+1192.63=-3007.37 cal

ΔUca=-3007.37 cal

c) Para todo el ciclo tendremos la variación de energía interna debe ser nula. Podemos comprobar que es prácticamente cierto:

ΔU=ΔUab+ΔUbc+ΔUca=3000+0-3007.37=-7.37 cal≈0

ΔU=0

La variación de calor:

ΔQ=ΔQab+ΔQbc+ΔQca=3000+1653.33-4200=453.33 cal

ΔQ=453.33 cal

Y la variación de trabajo:

ΔW=ΔWab+ΔWbc+ΔWca=0+1653.33-1192.63=460.07 cal

ΔW=460.07 cal

Podríamos haberlo determinado también mediante la aplicación del primer principio de la Termodinámica:

ΔQ=ΔU+ΔW=ΔW=453.33 cal