a) V1=7527.6 l
b) ΔWexpansión=9.83·106 J
c) ΔWcompresión=- 91.28·106 J
a) Tenemos el ciclo que aparece en la figura. Como datos conocemos:
T1=180ºC=453 K; T2=40ºC=313 K; n=2000 moles; Q1=40·105 J; P1=106 N/m2=9.87 atm
R=2 cal/molK; ![]() .
.
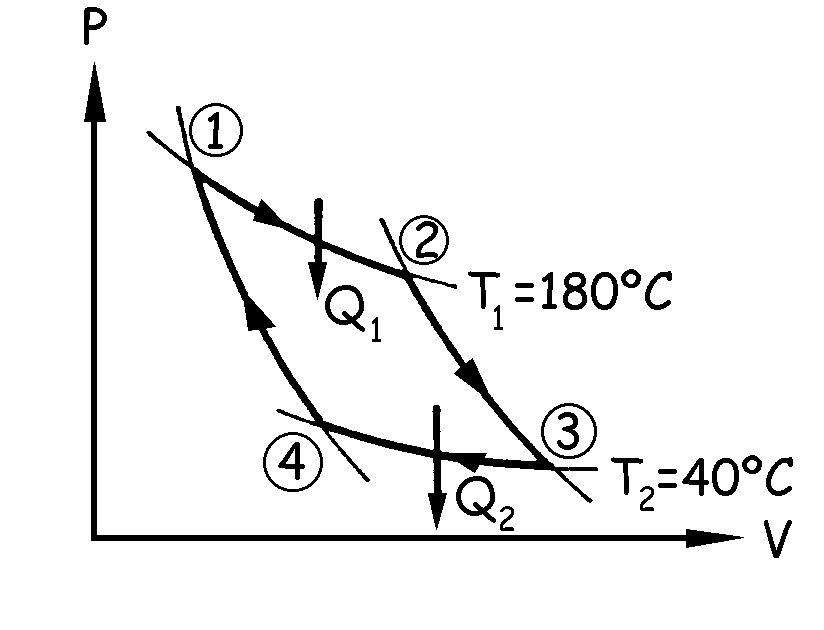 Nos piden el volumen del gas al iniciarse y al finalizar la compresión isoterma, es decir, el volumen del gas en el punto 1 y en el punto 2. Por ser un gas ideal tendremos:
Nos piden el volumen del gas al iniciarse y al finalizar la compresión isoterma, es decir, el volumen del gas en el punto 1 y en el punto 2. Por ser un gas ideal tendremos:
![]()
V1=7527.6 l
Como la transformación es isoterma ΔU12=0 y W12=Q1
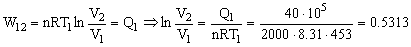
V2=12805.3 l
b) Se produce una expansión en las etapas 1—2 y 2—3. La transformación 1—2 es isoterma luego la variación de energía interna es nula:
ΔU12=0
Y aplicando el primer principio de la Termodinámica:
ΔQ12=ΔU12+ΔW12 ⇒ ΔW12=ΔQ12-ΔU12=ΔQ12=Q1=40 · 105 J
La transformación 2—3 es adiabática luego la variación de calor es nula:
ΔQ23=0
Y por el primer principio:
ΔQ23=ΔU23+ΔW23 ⇒ ΔW23=ΔQ23-ΔU23=-ΔU23=-ncVΔT23=-ncV(T3-T2)
El calor específico a volumen constante se puede obtener de la expresión:
cP-cV=R ⇒ cV=cP-R=7-2=5 cal/molK
Por tanto tendremos:
ΔW23=-ncV(T3-T2)=-2000 · 5(453-313)=1400000 cal=5.83·106 J
Entonces el trabajo realizado durante la expansión es:
ΔWexpansión=ΔW12+ΔW23=40·105+5.83·106=9.83 · 106 J
ΔWexpansión=9.83·106 J
c) La compresión se realiza en las etapas 3—4 y 4—1. La etapa 3—4 es una compresión isoterma luego la variación de energía interna es nula:
ΔU34=0
Por el primer principio de la Termodinámica:
ΔQ34=ΔU34+ΔW34 ⇒ ΔW34=ΔQ34-ΔU34=ΔQ34=Q2
Como tenemos un ciclo de Carnot la relación entre los calores intercambiados es:
![]()
Habrá que tener en cuenta que este calor tiene signo contrario al anterior, luego es negativo:
ΔW34=Q2=-2763796.91 J
La etapa 4—1 es una compresión adiabática luego la variación de calor es nula:
ΔQ41=0
Por el primer principio de la Termodinámica:
ΔQ41=ΔU41+ΔW41 ⇒ ΔW41=ΔQ41-ΔU41=-ΔU41=-ncVDT41=-ncV(T1-T4)
-2000·5(453-313)=-5852000 J
El trabajo realizado entonces durante la compresión es:
ΔWcompresión=ΔW34+ΔW41=-2763796.91-5852000=-61283796.91 J=-91.28·106 J
ΔWcompresión=- 91.28·106 J