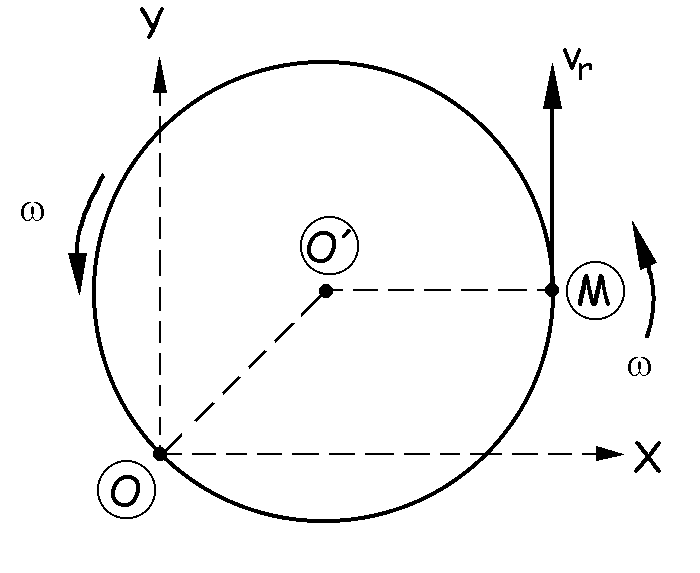
 Tendremos una mosca moviéndose con velocidad angular constante ω alrededor de un punto O’, y a su vez este punto O’ se mueve con la misma velocidad angular constante ω alrededor de un punto fijo O.
Tendremos una mosca moviéndose con velocidad angular constante ω alrededor de un punto O’, y a su vez este punto O’ se mueve con la misma velocidad angular constante ω alrededor de un punto fijo O.
La velocidad relativa vr es la que tiene la mosca en el sistema de referencia de la plataforma. Respecto de la plataforma, la mosca realiza un movimiento circular uniforme con centro en O’, luego la velocidad relativa será tangente a la trayectoria (la circunferencia externa de la plataforma) y su sentido el de avance de la mosca. Vectorialmente esta velocidad se puede poner como:
vr=ω X O’M
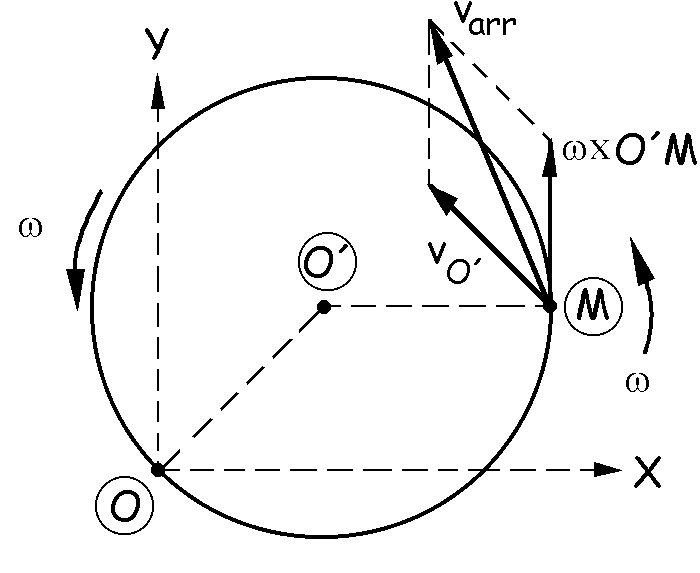 La velocidad de arrastre será:
La velocidad de arrastre será:
varr=vO’+ω X O’M
El punto O’ realiza un movimiento de rotación en torno a O luego su velocidad será tangente a la trayectoria descrita perpendicular a la recta O’O). El vector ω X O’M será, por provenir de un producto vectorial, perpendicular al plano formado por los dos vectores, y su sentido será el que da la regla de la mano derecha (sacacorchos). La velocidad de arrastre es pues la composición de estos dos vectores.
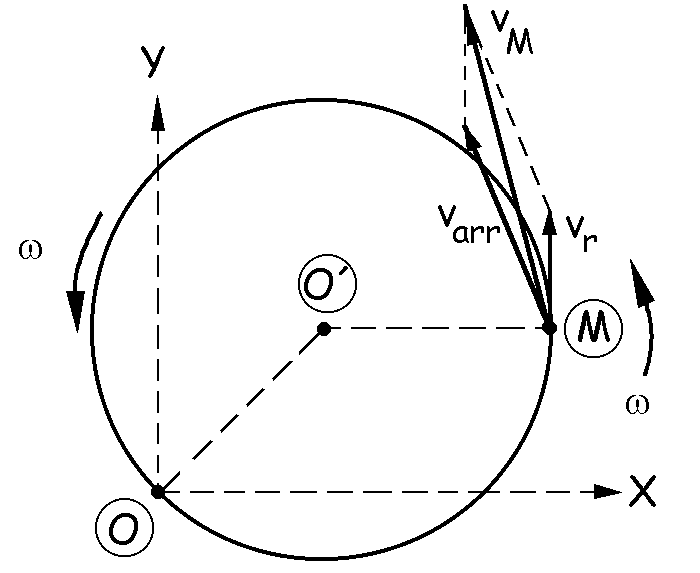 Y la velocidad absoluta será la composición de los vectores:
Y la velocidad absoluta será la composición de los vectores:
vM=vO’+ω X O’M=varr+vr
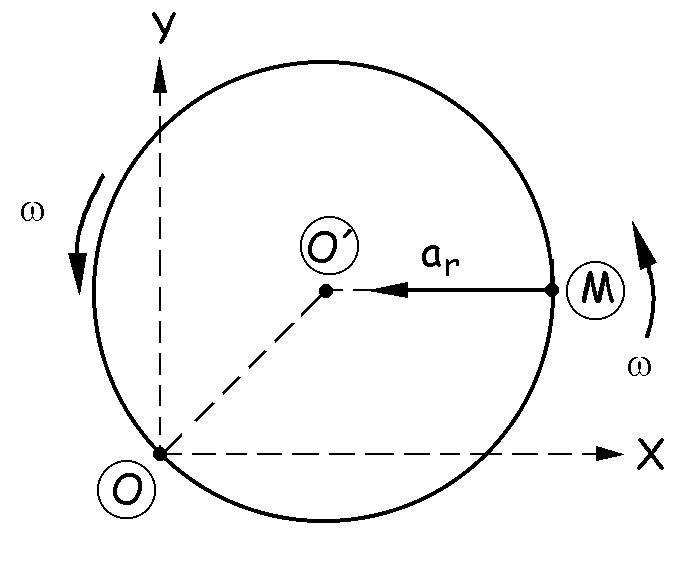 La aceleración relativa es la de la mosca en el sistema de referencia de la plataforma. Respecto de la plataforma, el movimiento es circular y uniforme, por lo que la única componente de la aceleración relativa sería la normal, en la dirección del radio de curvatura y apuntando hacia el centro de curvatura.
La aceleración relativa es la de la mosca en el sistema de referencia de la plataforma. Respecto de la plataforma, el movimiento es circular y uniforme, por lo que la única componente de la aceleración relativa sería la normal, en la dirección del radio de curvatura y apuntando hacia el centro de curvatura.
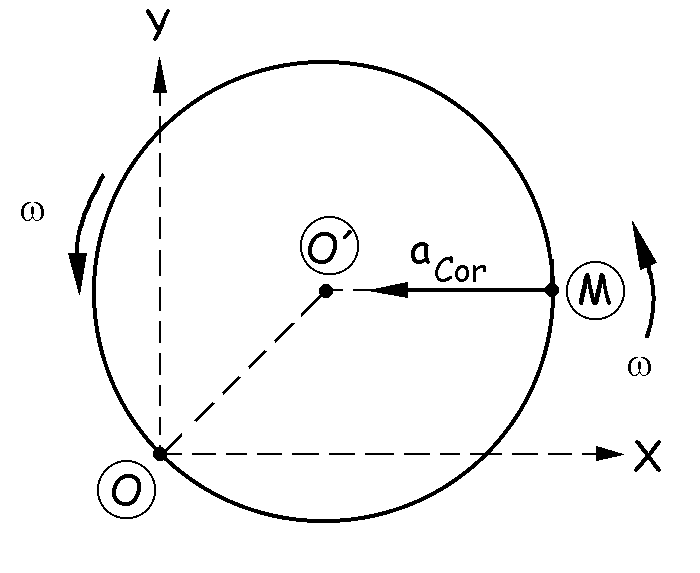 La aceleración de Coriolis vale:
La aceleración de Coriolis vale:
aCor=2ω X vr
El vector aceleración de Coriolis es por tanto un vector perpendicular al plano formado por los vectores ω y vr, y sentido el que indica la regla de la mano derecha.
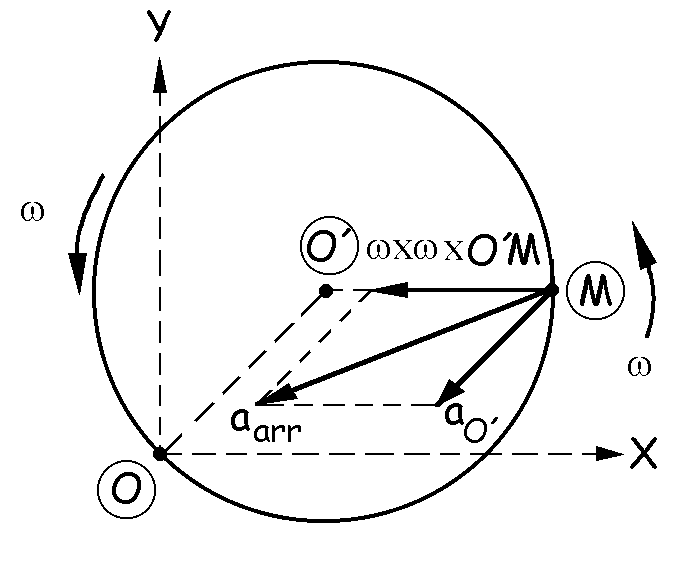 La aceleración de arrastre vale:
La aceleración de arrastre vale:
aarr=aO’+α X O’M+ω X ω X O’M
Como:
ω=cte ⇒ α=0
Con lo cual nos queda:
aarr=aO’+ω X ω X O’M
El punto O’ realiza un movimiento de rotación uniforme en torno a O, luego su aceleración, ao’, sólo tiene componente normal, en la dirección del radio de curvatura y apuntando hacia el centro de curvatura.
El vector ω X ω X O’M será perpendicular al plano formado por ω y ω X O’M (vector ya dibujado antes y que tenía la misma dirección y sentido que la velocidad relativa).
La aceleración de arrastre será la composición de estos dos vectores.
Y por último, la aceleración absoluta vale:
aM=aO’+α X O’M+ω X ω X O’M+2ω X vr+ar=aarr+aCor+ar
Tendríamos que componer estos tres vectores.