La resonancia en amplitud coincide con la resonancia en energía cinética sólo si el parámetro de amortiguamiento es muy pequeño y puede despreciarse frente a la frecuencia natural
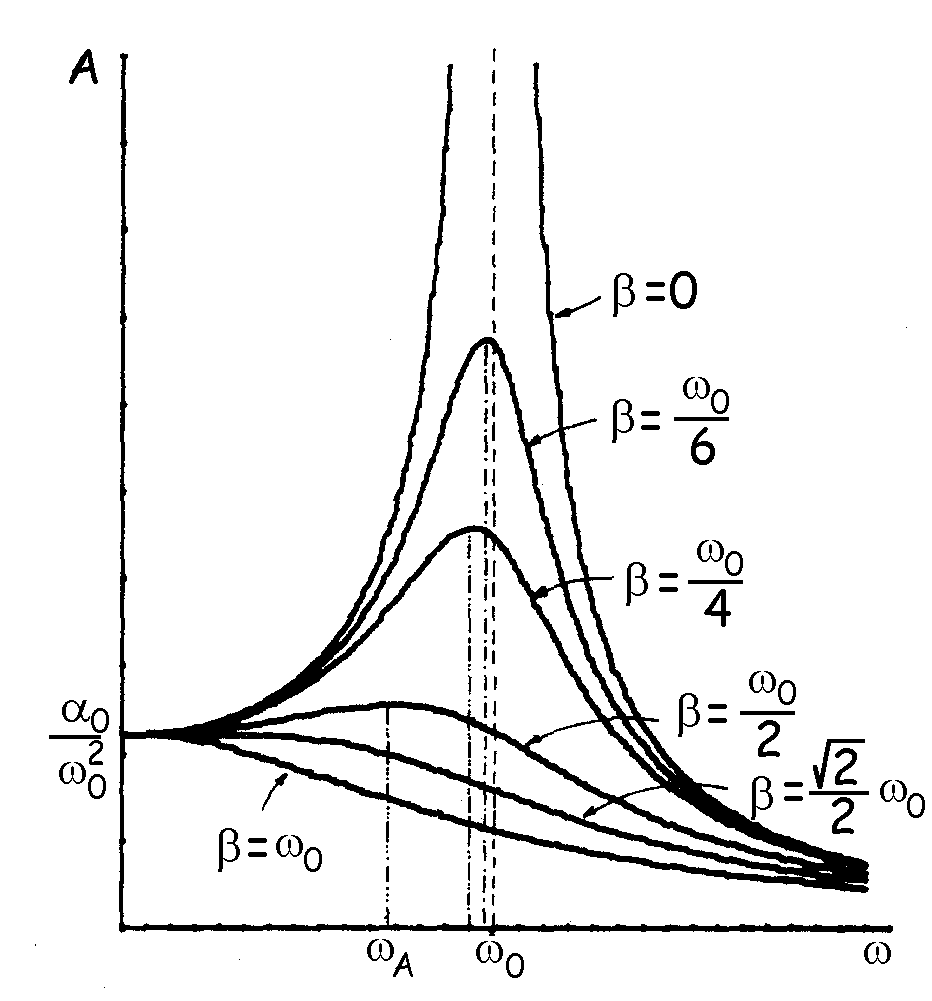La amplitud A de las oscilaciones forzadas es función de la frecuencia de la fuerza impulsora. En la figura se observa la función A(ω) para distintos valores del parámetro de amortiguamiento β. Para cada valor de β se puede determinar el valor de la frecuencia de la fuerza impulsora para el cual el valor de la amplitud alcanza su valor máximo. Llamaremos ωA a este valor. Para determinarlo, partiremos de la expresión que relaciona la amplitud con la frecuencia de la fuerza impulsora, que es:
Derivando esta expresión e igualando a cero el resultado:
para obtener:
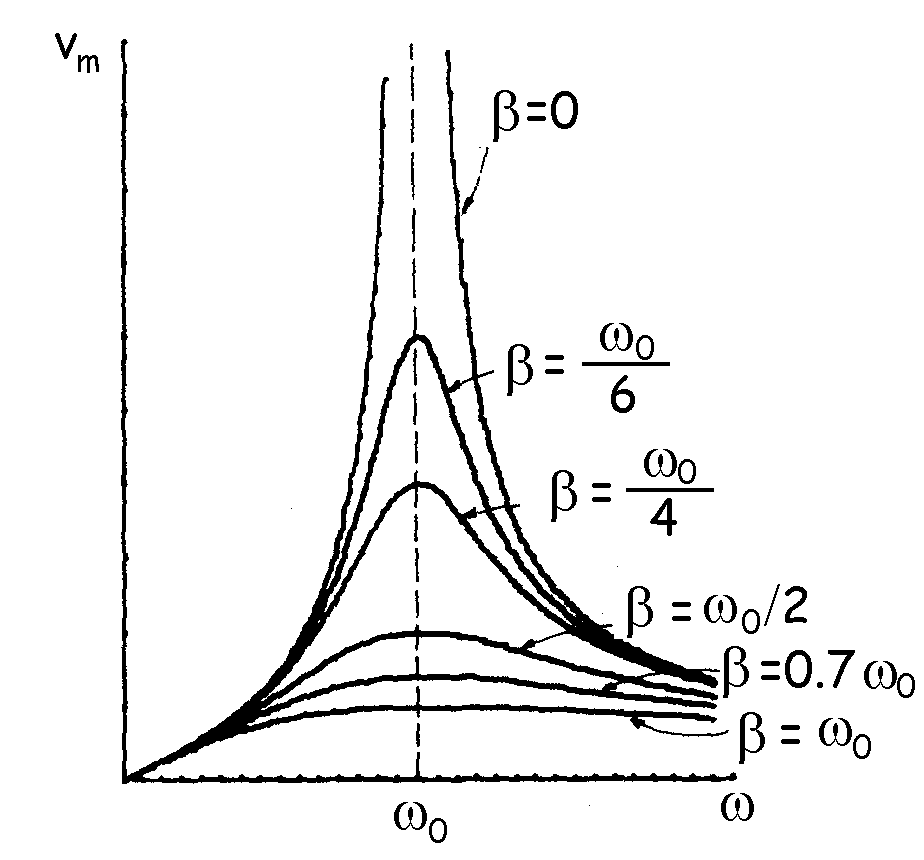La amplitud de la velocidad varía con la frecuencia impuesta como se indica en esta segunda figura. La amplitud de la velocidad, es decir, la velocidad máxima en cada ciclo es:
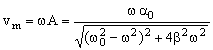
Como puede verse, vm presenta su valor máximo, para cualquier valor de β, cuando la frecuencia, a la que llamaremos ωv vale:
ωv=ω0
es decir, cuando se anula el paréntesis de la expresión anterior. A esta frecuencia, la velocidad y la energía cinética de la masa oscilante son máximas y hay resonancia en la energía cinética.
La resonancia en amplitud coincide con la resonancia en energía cinética sólo si el parámetro de amortiguamiento es muy pequeño y puede despreciarse frente a la frecuencia natural. En este caso tendremos:
