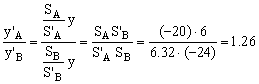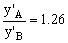a) ra1=2 cm, ra2=4 cm, rb1=4 cm, rb2=6 cm ó ra1=3.6 cm, ra2=7.2 cm, rb1=3.6 cm, rb2=2.4 cm
b) 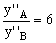
c) S’A=6.32 cm, S’B=6 cm, 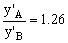
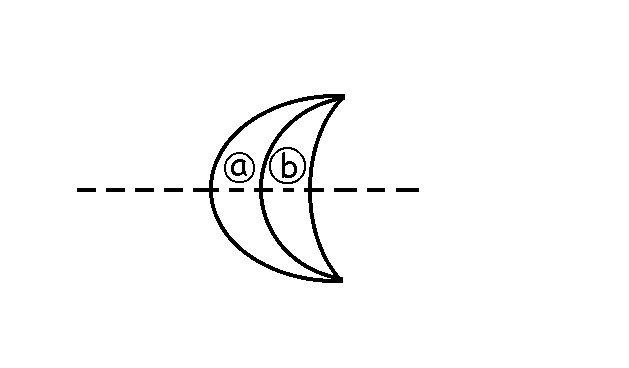 a) Tenemos una lente formada por dos lentes convergente convexo-cóncavas. La lente de índice de refracción 1.2, que llamaremos lente a, tiene los radios en proporción 1 a 2, luego tal como la hemos dibujado tendrá radios r y 2r. La otra lente, que llamaremos lente b, podemos situarla a la izquierda o a la derecha de ésta. Empecemos por ponerla a la derecha. Dado que los radios de esta segunda lente deben estar en proporción 2 a 3, no hay más posibilidad que el que sean 2r y 3r. Como las lentes son yuxtapuestas, las potencias son aditivas. Entonces:
a) Tenemos una lente formada por dos lentes convergente convexo-cóncavas. La lente de índice de refracción 1.2, que llamaremos lente a, tiene los radios en proporción 1 a 2, luego tal como la hemos dibujado tendrá radios r y 2r. La otra lente, que llamaremos lente b, podemos situarla a la izquierda o a la derecha de ésta. Empecemos por ponerla a la derecha. Dado que los radios de esta segunda lente deben estar en proporción 2 a 3, no hay más posibilidad que el que sean 2r y 3r. Como las lentes son yuxtapuestas, las potencias son aditivas. Entonces:
![]()
![]()
Por tanto, para el menisco convergente a, los radios de curvatura son:
ra1=r=2 cm; ra2=2r=2 · 2=4 cm
ra1=2 cm
ra2=4 cm
Y para el menisco convergente b:
rb1=2r=2·2=4 cm; rb2=3r=3 · 2=6 cm
rb1=4 cm
rb2=6 cm
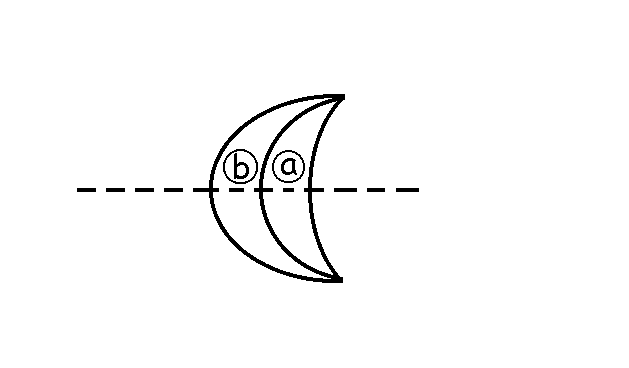 Ahora vamos a situar la lente b a la izquierda de la lente a. En este caso, como los radios de curvatura de la lente b están en la relación 2 a 3, dichos radios serán 2r/3 y r. Tendremos entonces, haciendo como antes:
Ahora vamos a situar la lente b a la izquierda de la lente a. En este caso, como los radios de curvatura de la lente b están en la relación 2 a 3, dichos radios serán 2r/3 y r. Tendremos entonces, haciendo como antes:
![]()
![]()
Entonces en este segundo caso, para el menisco convergente a los radios serán:
ra1=r=3.6 cm; ra2=2r=2 · 3.6=7.2 cm
ra1=3.6 cm
ra2=7.2 cm
Y para el menisco convergente b:
rb1=r=3.6 cm; ![]()
rb1=3.6 cm
rb2=2.4 cm
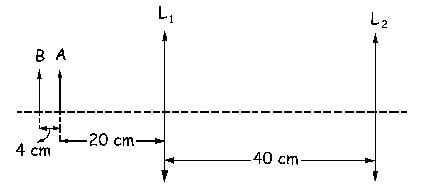
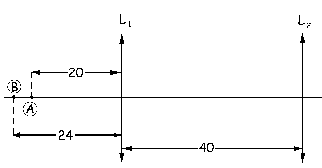
b) Tenemos en primer lugar el sistema que aparece en la figura. Empezaremos por determinar la imagen del objeto A. En primer lugar actúa la lente L1, para la cual A es el objeto y A’ será la imagen. Entonces:
![]()
S’A=30 cm
La distancia imagen sale positiva, lo que implica que la imagen A’ está a la derecha de L1 y a 30 cm de ella. Dicha imagen será el objeto de L2. Respecto de esta lente tendremos:
SA’=-(40-30)=-10 cm
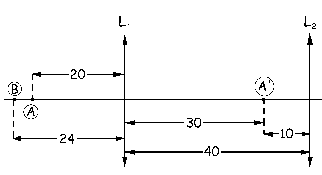
Y para esta lente tenemos:
![]()
S’A’=40 cm
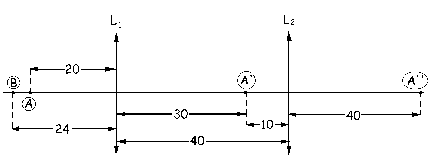
La imagen final A» está a la derecha de L2 y a 40 cm de ella. Vamos a ver cuál sería el tamaño respecto del objeto. El aumento lateral para el punto A será:
![]()
![]()
El aumento lateral es también la relación entre el tamaño de la imagen y el tamaño del objeto luego:
![]()
siendo y el tamaño del objeto, que será igual para B puesto que los objetos son idénticos.
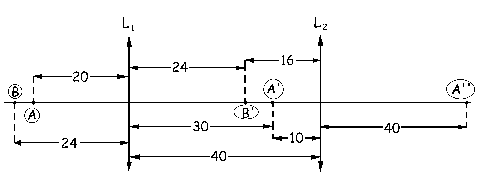
Pasamos ahora al objeto B. Primero actuará la lente L1, para la cual el objeto es B y la imagen B’. Aplicando la ecuación de las lentes delgadas:
![]()
![]()
La imagen B’ está a la derecha de L1 y a 24 cm de ella. Respecto de L2, que es la lente que actúa a continuación, tendremos:
SB’=-(40-24)=-16 cm
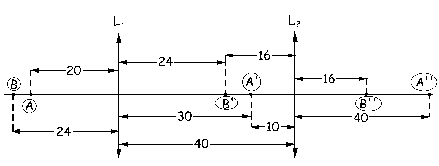
A continuación actúa la lente L2, para la cual el objeto es B’ y la imagen B». Para esta lente:
![]()
![]()
Por tanto la imagen final de B está a la derecha de L2 y a 16 cm de ella. Para este objeto el aumento lateral es:
![]()
Y teniendo en cuenta que el aumento lateral es la relación entre el tamaño de la imagen y el tamaño del objeto, y que el tamaño de B y A son iguales (y):
![]()
Entonces la relación entre las dos imágenes:
![]()
La imagen de A es 6 veces mayor que la imagen de B:
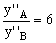
c) Ahora desplazamos la lente L2 hasta que queda en contacto con L1. Como están en contacto tendríamos un caso de lentes yuxtapuestas, es decir, las potencias pueden sumarse. El sistema de dos lentes será equivalente a una única lente cuya distancia focal vale F’:
![]()
Entonces es como si tuviéramos una única lente de distancia focal 4.8 cm. Para el objeto A:
![]()
S’A=6.32 cm
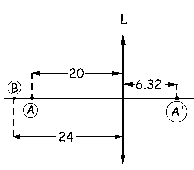
A través del aumento lateral podemos determinar el tamaño de la imagen:
![]()
Y para el objeto B:
![]()
S’B=6 cm
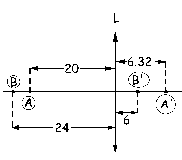
Y el tamaño de dicho objeto:
![]()
La relación entre los tamaños es entonces: