2dsenθ=mλ (m=1, 2, 3, …)

Cuando pasan rayos X por un cristal, el patrón de intensidad de los rayos dispersados a lo largo de la dirección de observación es el resultado de la interferencia de las ondas dispersadas por cada átomo en esa dirección, modulado por un factor de dispersión característico de los átomos. En este sentido, el cristal es análogo a una rejilla tridimensional en la que la difracción de cada ranura se sustituye por la dispersión atómica.

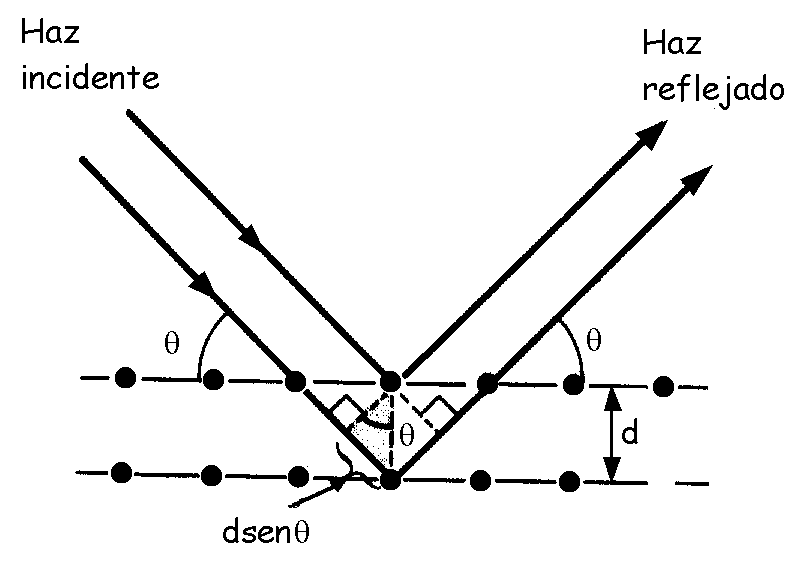Consideramos un haz de rayos X que incide formando un ángulo θ con uno de los planos de átomos que forman el cristal. El haz puede reflejarse en ambos planos, el superior y el inferior, los cuales contienen a los átomos. Sin embargo, la geometría de la figura muestra que el haz reflejado en el plano inferior viaja una distancia mayor que el reflejado en el plano superior.

La diferencia de camino efectiva entre los dos haces es 2dsenθ. Los haces se refuerzan entre sí (interferencia constructiva) cuando la diferencia de caminos es igual a múltiplos enteros de la longitud de onda. Por lo tanto, la condición de interferencia constructiva está dada por:

2dsenθ=mλ (m=1, 2, 3, …)

Esta relación se conoce como ley de Bragg en honor de W. L. Bragg (1890-1971), quien fue el primero en obtenerla.