a) vA=7688.54 m/s, T=5532.54 s
b) v0=3912.9 m/s
c) ΔvA=4727.42 m/s
a) Tenemos los datos:
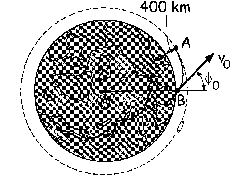
rA=hA+RT=400+6370=6770 km
rB=hB+RT=45+6370=6415 km
La estación espacial se encuentra en una órbita circular, por lo que la única fuerza que experimenta es la de atracción gravitatoria y la única aceleración que tiene es la normal, ya que el movimiento es circular uniforme. Teniendo en cuenta que esta fuerza y esta aceleración tienen la misma dirección y sentido y aplicando la segunda ley de Newton:
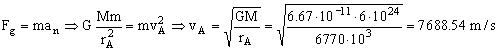
vA=7688.54 m/s
Y mediante la tercera ley de Kepler podemos determinar el período de la órbita, ya que los cuadrados de los períodos son directamente proporcionales a los cubos de los semiejes mayores (en el caso de una órbita circular de los radios):
![]()
T=5532.54 s
b) En la trayectoria AB se deben conservar tanto el momento angular como la energía total, ya que nos encontramos ante un caso de fuerzas centrales. Llamaremos v’A a la velocidad de la lanzadera en el punto A, correspondiente a la órbita de transición (no a la circular). Tendremos por tanto que por la conservación del momento angular:
LA=LB ⇒ mrAv’AsenφA=mrBvBsenφB
En el punto A la velocidad es perpendicular al radio vector por lo que:
φA=90º ⇒ senφA=sen90º=1
Entonces:
mrAv’AsenφA=mrBvBsenφB ⇒ rAv’A=rBvBsenφB
![]()
Y además se debe conservar la energía total, luego:
![]()
Sustituimos v’A por su valor:
![]()
![]()
v0=3912.9 m/s
c) Para que la lanzadera se acople a la estación debe igualar su velocidad. La velocidad de la lanzadera al llegar a A es:
v’A=0.757v0=0.757 · 3912.9=2961.12 m/s
Y debe llegar a la velocidad de la estación, que es:
vA=7688.54 m/s
El incremento de velocidad será por tanto:
ΔvA=vA-v’A=7688.54-2961.12=4727.42 m/s
ΔvA=4727.42 m/s