a) vB=15 m/s; aB=514.85 m/s2
b) P=30.6 N; Q=-62.2 N
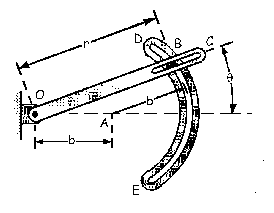
Esquemáticamente tenemos lo que aparece en la figura.
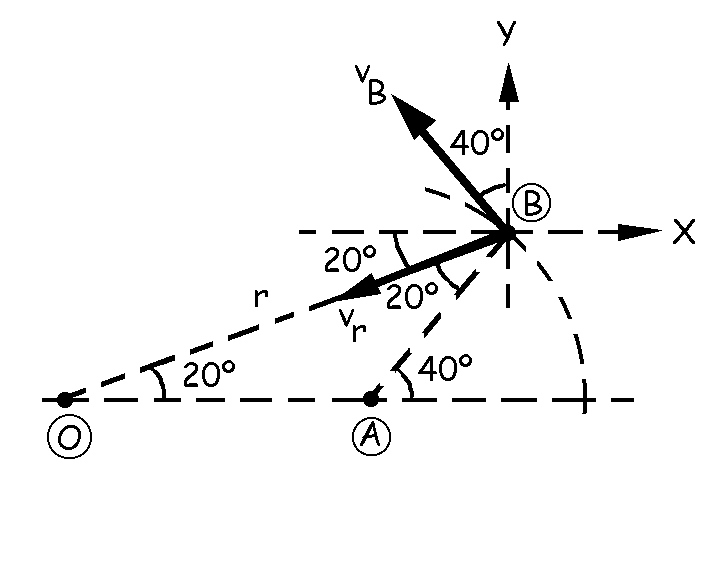
La velocidad del punto B será:
vB=vO+ω x OB+vr
Como el punto O es un punto fijo:
vO=0 ⇒ vB=vO+ω x OB+vr=ω x OB+vr
Obviamente:
![]()
El valor del vector OB en módulo será, aplicando el teorema del coseno:
![]()
Y vectorialmente:
OB=OBcos20i+OBsen20j=0.94cos20i+0.94sen20j=0.883i+0.321j
El punto B está obligado a moverse en una ranura circular, luego la velocidad será tangente a la trayectoria:
vB=-vBsen40i+vBcos40j
La velocidad relativa es la que tiene el punto en el sistema de referencia móvil, es decir, en la ranura. Como es una ranura recta la velocidad relativa debe tener la dirección de la ranura. El sentido le suponemos arbitrario. Entonces:
vr=-vrcos20i-vrsen20j
Sustituyendo todo:
vB=ω x OB+vr ⇒

-vBsen40i+vBcos40j=13.245j-4.815i-vrcos20i-vrsen20j
Igualamos por separado las componentes en X y las componentes en Y:
Eje X: -vBsen40=-4.815-vrcos20
Eje Y: vBcos40=13.245-vrsen20
Dividiendo las dos ecuaciones:
![]()
Como la velocidad relativa sale positiva significa que el sentido que elegimos para ella arbitrariamente es el correcto.
La velocidad de B la podemos despejar de cualquiera de las dos ecuaciones. Por ejemplo, a partir de la ecuación del eje Y:
vBcos40=13.245-vrsen20 ⇒
![]()
vB=15 m/s
Podríamos determinar esta velocidad en coordenadas polares, que sería mucho más sencillo. En polares tendremos:
![]()
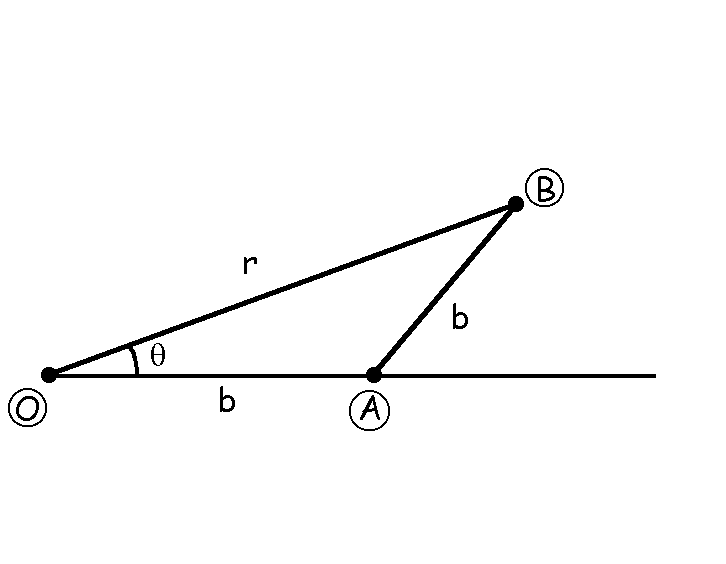
Tenemos un triángulo isósceles, el triángulo OAB. En él podemos ver que se cumple que:
r=bcosθ+bcosθ ⇒ r=2bcosθ
En esta ecuación podemos determinar también r:
r=2bcosθ=2 · 0.5cos20=0.94 m
Derivando una vez respecto del tiempo:
![]()
 Podemos ver que este resultado es la velocidad relativa que habíamos determinado de la otra forma. La velocidad de B será entonces:
Podemos ver que este resultado es la velocidad relativa que habíamos determinado de la otra forma. La velocidad de B será entonces:
![]()
Y en módulo tendremos:
![]()
vB=15 m/s
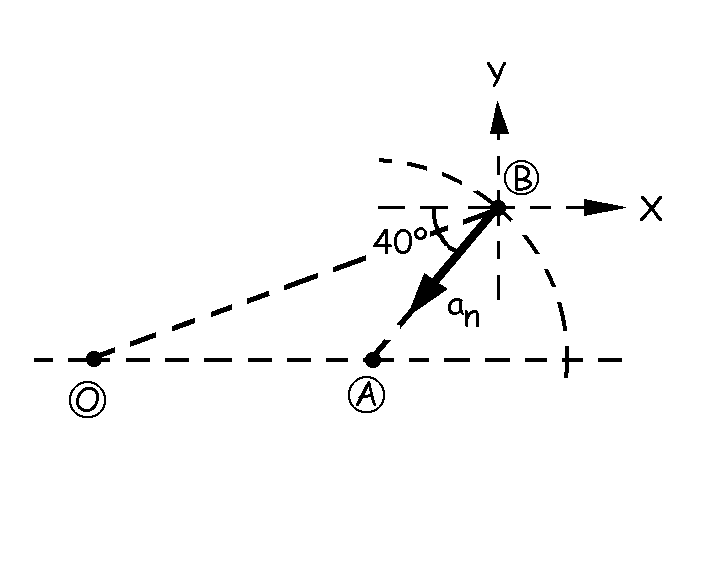 Ahora vamos a determinar la aceleración del punto B. Como está obligado a moverse en una ranura circular tendrá dos componentes de aceleración, la normal y la tangencial. Conocemos la aceleración normal, que será el módulo de la velocidad al cuadrado partido por el radio de curvatura:
Ahora vamos a determinar la aceleración del punto B. Como está obligado a moverse en una ranura circular tendrá dos componentes de aceleración, la normal y la tangencial. Conocemos la aceleración normal, que será el módulo de la velocidad al cuadrado partido por el radio de curvatura:
![]()
En cuanto a su dirección y sentido, será el del radio de curvatura y apuntando hacia el centro de curvatura, es decir, dirección BA:
an=-ancos40i-ansen40j=-450cos40i-450sen40j=-344.72i-289.25j
La aceleración tangencial será, como su nombre indica, tangente a la trayectoria, luego tiene la misma dirección que la velocidad. Supondremos además que su sentido es también el mismo, luego:
at=-atsen40i+atcos40j
Por tanto la aceleración del punto B será:
aB=an+at=-344.72i-289.25j-atsen40i+atcos40j
Por otro lado, en función del punto O podemos escribir:
aB=aO+a x OB-ω2OB+2ω x vr+ar
Como el punto O es un punto fijo:
aO=0 ⇒ aB=aO+a x OB-ω2OB+2ω x vr+ar=a x OB-ω2OB+2ωx vr+ar
La aceleración angular será:
![]()
Vectorialmente tenemos que la velocidad relativa será:
vr=-vrcos20i-vrsen20j=-5.13cos20i-5.13sen20j=-4.82i-1.75j
Y la aceleración relativa será la que tiene el punto B respecto del sistema móvil, es decir, respecto de la ranura recta. Esta aceleración tendrá que tener la dirección de la ranura, y además supondremos por comodidad que su sentido es el mismo que el de la velocidad relativa:
ar=-arcos20i-arsen20j
Sustituyendo todo tendremos:
aB=a x O
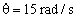 y
y  para la posición θ=20o, hallar en ese instante: a) la velocidad y aceleración del pasador B; b) las fuerzas P y Q ejercidas sobre B por la varilla OC y la ranura DE respectivamente.
para la posición θ=20o, hallar en ese instante: a) la velocidad y aceleración del pasador B; b) las fuerzas P y Q ejercidas sobre B por la varilla OC y la ranura DE respectivamente.