a) ν’=530.10 Hz
b) x=5 m y cada 0.349 m a ambos lados del punto central
c) h=3.35 cm
d) Séptimo Armónico
e) h=28.2 cm
a) En primer lugar tendremos que determinar la velocidad de las ondas sonoras en el aire, que llamaremos v0, a la temperatura que nos interesa.
Conocemos la temperatura a T0=0ºC=273 K. Para un gas ideal:
![]()
donde γ es el coeficiente adiabático de los gases, R la constante de los gases perfectos, T0 la temperatura y M la masa molecular del gas. Buscamos la velocidad de las ondas a temperatura T=15ºC=288 K. Aplicamos la misma ecuación a esta temperatura y tendremos:
![]()
Dividiendo ambas expresiones:
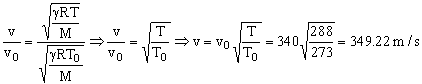
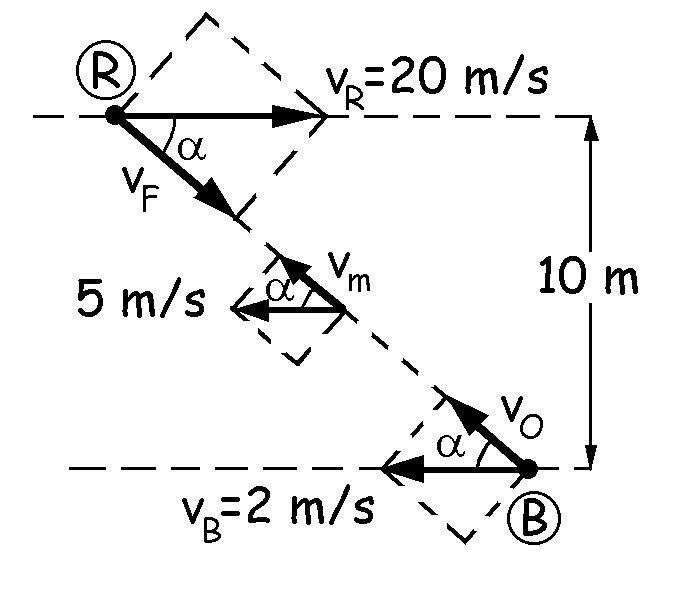 Ahora tenemos un problema de efecto Doppler. Roger Rabitt y Betty Boop se están acercando, luego tendremos lo que aparece en la figura. El ángulo α podemos determinarlo a través de la tangente, teniendo en cuenta que la recta que separa los puntos R y B mide 20 m:
Ahora tenemos un problema de efecto Doppler. Roger Rabitt y Betty Boop se están acercando, luego tendremos lo que aparece en la figura. El ángulo α podemos determinarlo a través de la tangente, teniendo en cuenta que la recta que separa los puntos R y B mide 20 m:
![]()
Ahora tenemos un problema de efecto Doppler, donde el observador sería Betty y la fuente sería Roger. La frecuencia percibida será:
![]()
En esta ecuación tenemos que proyectar todas las velocidades sobre la recta que une el observador con la fuente, y tomar como sentido positivo el que va desde la fuente hasta el observador. Haciendo esto nos queda:
![]()
ν‘=530.10 Hz
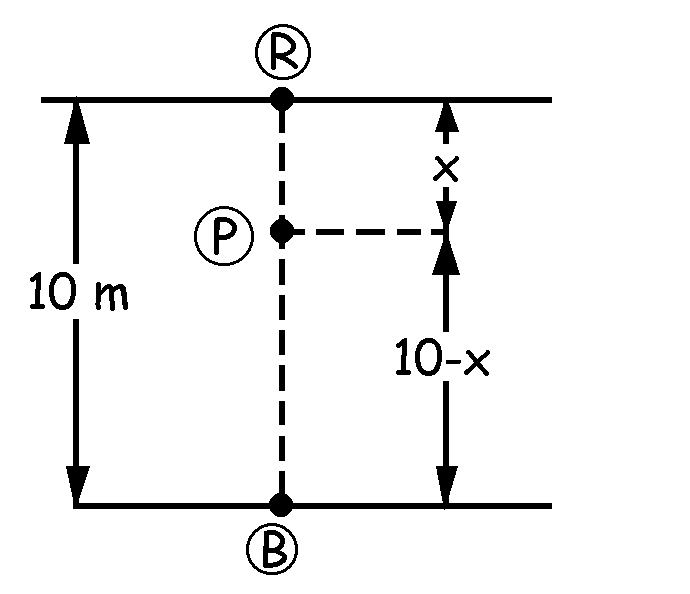 b) A continuación Roger y Betty se sitúan enfrentados, y ambos emiten una onda de frecuencia 500 Hz. Supongamos que se produce un máximo en el punto P. La interferencia se produce porque al punto P llegan dos ondas que recorren caminos diferentes, y que por tanto se desfasan. Lógicamente tendremos un máximo en el centro de las dos calles, a una distancia de 5 m de cualquiera de ellos, ya que en ese punto la diferencia de caminos recorridos es nula (las dos ondas recorren el mismo camino) y las ondas llegarían en fase. Entonces el único problema consiste en determinar la distancia entre dos máximos consecutivos. Sabiendo esto, tendremos que se producen máximos en el centro de las dos calles y a ambos lados de ese punto a intervalos regulares correspondientes a la distancia entre dos máximos. Para un punto P se producirá un máximo cuando el desfase sea un número par de veces π:
b) A continuación Roger y Betty se sitúan enfrentados, y ambos emiten una onda de frecuencia 500 Hz. Supongamos que se produce un máximo en el punto P. La interferencia se produce porque al punto P llegan dos ondas que recorren caminos diferentes, y que por tanto se desfasan. Lógicamente tendremos un máximo en el centro de las dos calles, a una distancia de 5 m de cualquiera de ellos, ya que en ese punto la diferencia de caminos recorridos es nula (las dos ondas recorren el mismo camino) y las ondas llegarían en fase. Entonces el único problema consiste en determinar la distancia entre dos máximos consecutivos. Sabiendo esto, tendremos que se producen máximos en el centro de las dos calles y a ambos lados de ese punto a intervalos regulares correspondientes a la distancia entre dos máximos. Para un punto P se producirá un máximo cuando el desfase sea un número par de veces π:
![]()
El máximo siguiente será de orden n+1 y se producirá a una distancia x’ que cumplirá que:
![]()
La distancia entre dos máximos será entonces:
![]()
Como cabía esperar la diferencia de distancia entre dos máximos consecutivos es una semilongitud de onda. Tendremos pues:
![]()
Por tanto tendremos máximos en x=5 m y a ambos lados de este punto cada 0.349 m.
x=5 m y cada 0.349 m a ambos lados del punto central
c) Ahora tenemos que la temperatura es de 25ºC, luego la velocidad de las ondas sonoras será:
![]()
Cuando se oye el primer pitido intenso tendremos como columna de aire la mayor posible. Por tratarse de un tubo cerrado por un extremo:
![]()
donde el término (2n+1) es un número impar. Dicho número será:
![]()
Poniendo l=lmáx=0.3 m podemos aproximar el máximo número impar que podemos tener:
![]()
Por tanto, el número impar más grande que podemos tener que cumple la condición de ondas estacionarias en el tubo es: 2n+1=15
Sustituyendo la longitud de tubo de aire es:
![]()
Si tenemos esta columna de aire, el resto hasta 0.3 m será de cerveza, es decir:
h=0.3-l=0.3-0.266=0.0335 m=3.35 cm
h=3.35 cm
d) Tenemos que: 2n+1=15 ⇒ n=7
Entonces, con n=0 tenemos el tono fundamental, con n=1 el primer armónico, con n=2 el segundo armónico, luego con n=7 tendremos el séptimo armónico.
SÉPTIMO ARMÓNICO
e) Para que se produzca el tono fundamental deberá verificarse que la longitud de aire sea:
![]()
Por tanto la altura de cerveza será el resto:
h=0.3-l=0.3-0.0178=0.282 m=28.2 cm
h=28.2 cm