Problema de Teoría Cinética de los Gases

Aparece en la convocatoria SEP1999

Un cilindro de paredes impermeables al calor está dividido en tres compartimentos, A, B y C por dos pistones, M1 y M2 móviles reversiblemente y sin rozamientos. Cada compartimento contiene 1 mol de gas perfecto diatómico, siendo inicialmente la presión en los tres compartimentos igual, P0=105 N/m2 y la temperatura en los tres T0=300 K. En el compartimento A hay una resistencia eléctrica de capacidad calorífica despreciable, que calienta muy lentamente el gas hasta que la temperatura en C es de 360 K. Determinar la presión, el volumen y la temperatura final en los tres compartimentos, así como el calor suministrado por la resistencia en el siguiente caso: el pistón M1 es adiabático (impermeable al calor) y el M2 es diatérmico (permeable al calor)
Tómese: 1 atm=101324.72 N/m2; R=2 cal/molK=0.082 atml/Kmol.

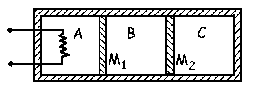
TA=983.89 K; TB=TC=360 K; VA=43.19 l; VB=VC=15.80 l; PA=PB=PC=1.893·105 N/m2; Q=16801.3 J

Tenemos como datos las condiciones iniciales en los tres compartimentos:

P0A=P0B=P0C=P0=105 N/m2=0.987 atm; T0A=T0B=T0C=T0=300 K; nA=nB=nC=n=1 mol

Como inicialmente la presión, la temperatura y el número de moles son iguales en los tres compartimentos, también serán iguales los tres volúmenes.

V0A=V0B=V0C=V0

Podemos determinar por tanto el volumen inicial en uno cualquiera de los tres compartimentos. Aplicando la ecuación de los gases perfectos:

Los tres pistones deslizan sin rozamiento, luego siempre las presiones finales serán iguales en los tres compartimentos:

PA=PB=PC

Como el pistón M2 es diatérmico, la temperatura final de los compartimentos B y C será la misma:

TB=TC=360 K

TB=360 K

TC=360 K

En los compartimentos B y C tenemos la misma presión, el mismo número de moles y la misma temperatura, luego tendremos también el mismo volumen:

VB=VC

Además el pistón M1 es adiabático, luego en el compartimento B+C la transformación es adiabática. Podemos considerar un único compartimento de volumen VB+VC=2VC a temperatura TC que experimenta una transformación adiabática, luego:

TVγ-1=cte

Determinamos los calores específicos y el coeficiente adiabático. Por ser gases ideales diatómicos:

Y sabemos que:

CP-CV=R ⇒ CP=R+CV=2+5=7 cal/molK

Por tanto el coeficiente adiabático es:

Tendremos entonces que para el compartimento B+C:

TVγ-1=cte

VC=15.80 l

Y entonces:

VB=VC=15.80 l

VB=15.80 l

El volumen total de los compartimentos A, B y C no cambia, y vale 3V0. Por tanto para el volumen del compartimento A después de la transformación tendremos:

3V0=VA+VB+VC ⇒ VA=3V0-VB-VC=3·24.93-15.80-15.80=43.19 l

VA=43.19 l

En el compartimento B conocemos el volumen, la temperatura y el número de moles, luego podemos determinar la presión a través de la ecuación de los gases perfectos:

PB=1.893·105 N/m2

Las presiones finales en los tres compartimentos son iguales, luego:

PA=1.893·105 N/m2

PC=1.893·105 N/m2

Nos falta únicamente la temperatura en el compartimento A, donde conocemos presión, volumen y número de moles. A partir de la ecuación de los gases perfectos:

TA=983.89 K

El sistema total (A+B+C) tiene volumen constante. Para una transformación isocora el trabajo realizado es nulo:

W=0

Por el primer principio de la termodinámica:

U=Q-W=Q

Por tanto el calor suministrado al sistema en este caso tiene que coincidir con la variación de energía interna:

Q=U=UA+UB+UC

Si tomamos el compartimento B+C la transformación es adiabática, luego:

QB+C=0

A través del primer principio de la Termodinámica:

UB+C=QB+C-WB+C=-WB+C=-2nCV(T0-TC)=-2 · 1 · 5(300-360)=600 cal=2508 J

Y para el compartimento A:

UA=nCV(TA-T0)=1 · 5(983.89-300)=3419.45 cal=14293.3 J

Entonces:

Q=UA+UB+UC=UA+UB+C=14293.3+2508=16801.3 J

Q=16801.3 J