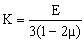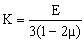
Consideremos un material en forma de cubo, de lado l, sumergido en un fluido, y por tanto sometido a una presión P. De esta forma, sobre cada una de sus caras actúa una fuerza compresiva de valor:
![]()
siendo A el área de cada una de las caras. Esta fuerza es igual en las tres direcciones del espacio (FX=FY=FZ=F) ya que la presión del fluido es la misma en todas las direcciones.
Debido a estas fuerzas compresivas, el material experimenta cambios en sus dimensiones. Trabajando siempre en la zona elástica, podemos relacionar estos cambios con el módulo de Young y el coeficiente de Poisson:
![]()
![]()
![]()
donde hemos tenido ya en cuenta que las fuerzas en las tres direcciones del espacio son iguales y que el área de cada cara es la misma. Introduciremos además al final el signo negativo correspondiente a fuerzas compresivas. Así, los cambios unitarios de longitud son iguales en las tres direcciones del espacio:
![]()
El cambio en las dimensiones del paralelepípedo irá acompañado de un cambio de volumen. Si las dimensiones originales de las aristas eran l, el volumen inicial del cubo será:
V=l3
Calculando la diferencial del volumen tendremos:
dV=3l2dl
Y la variación relativa de volumen será:
![]()
Si consideramos las deformaciones unitarias uniformes, podemos sustituir los diferenciales por incrementos finitos y tendremos:
![]()
Teniendo en cuenta que hay que poner signo negativo, ya que las fuerzas son compresivas (el volumen disminuye):
![]()
El módulo de compresibilidad de un material, K, es el cociente, cambiado de signo, entre la presión que actúa sobre él y la variación unitaria de volumen correspondiente:
![]()
Podemos escribir por tanto:
![]()