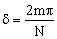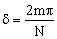
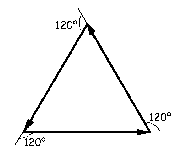
Podemos determinar la amplitud resultante sumando fasorialmente las contribuciones individuales. Puesto que las fuentes son idénticas, los fasores individuales tienen todos la misma longitud (misma amplitud) pero cada fasor presenta un adelanto de fase δ, es decir, está girado un ángulo δ respecto al anterior. En primer lugar vemos tres fuentes, es decir, tres fasores idénticos, con un desfase cada uno de ellos de 120º. Podemos ver que forman un triángulo cerrado, de modo que la suma de ellos es nula.
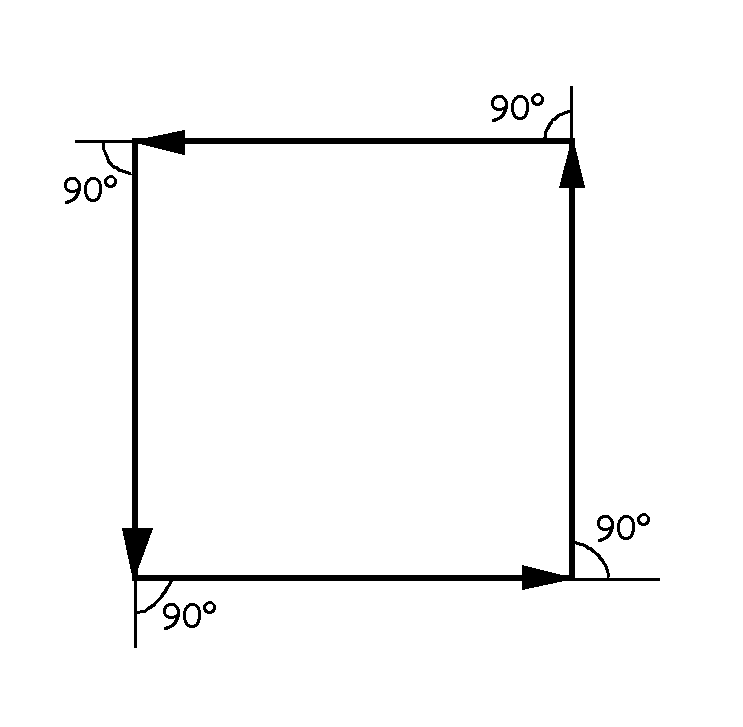
Lo mismo obtenemos con cuatro fasores desfasados 90º. Al colocar uno a continuación de otro para sumarlos podemos ver que forman un cuadrado (polígono cerrado), lo que implica que su suma también es nula.
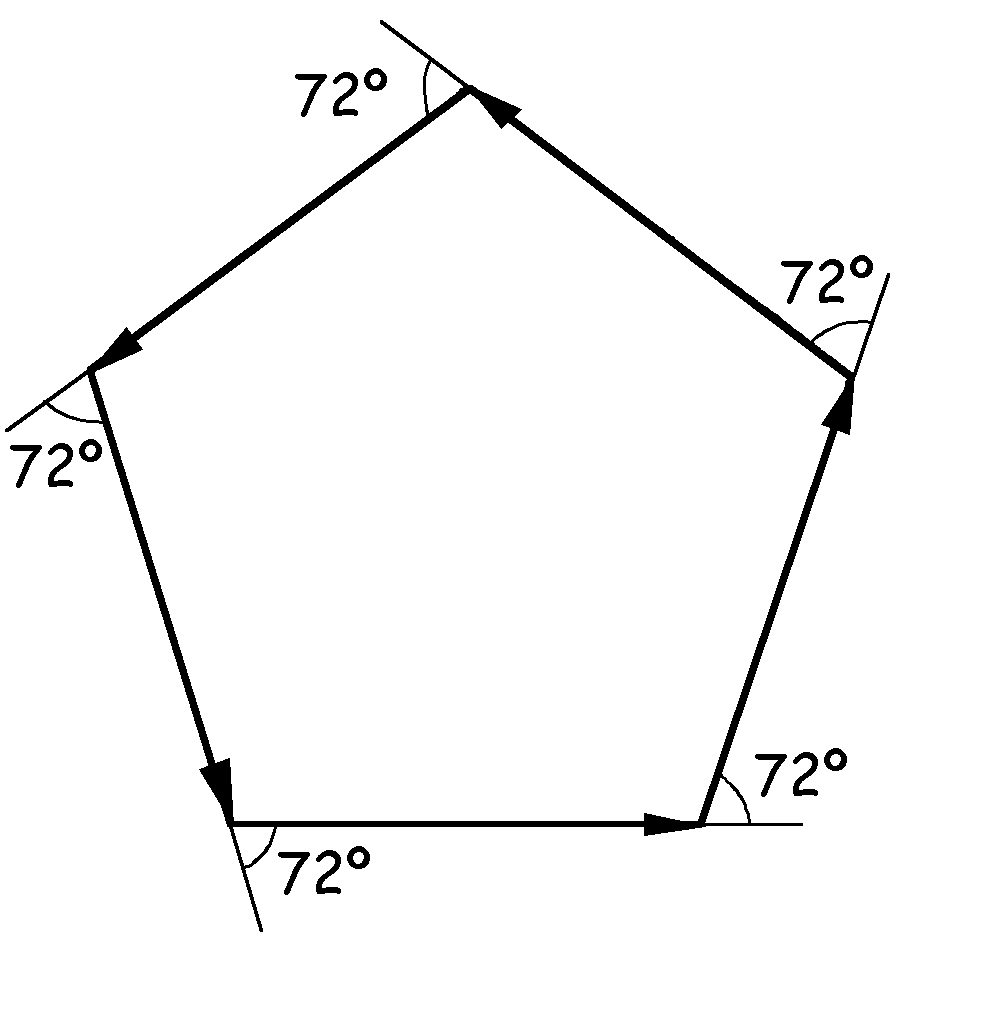
Por último tenemos lo mismo en el caso de cinco fasores desfasados 72º, obteniendo un polígono cerrado, en este caso un pentágono. En cualquiera de los tres casos la suma de los fasores es nula.
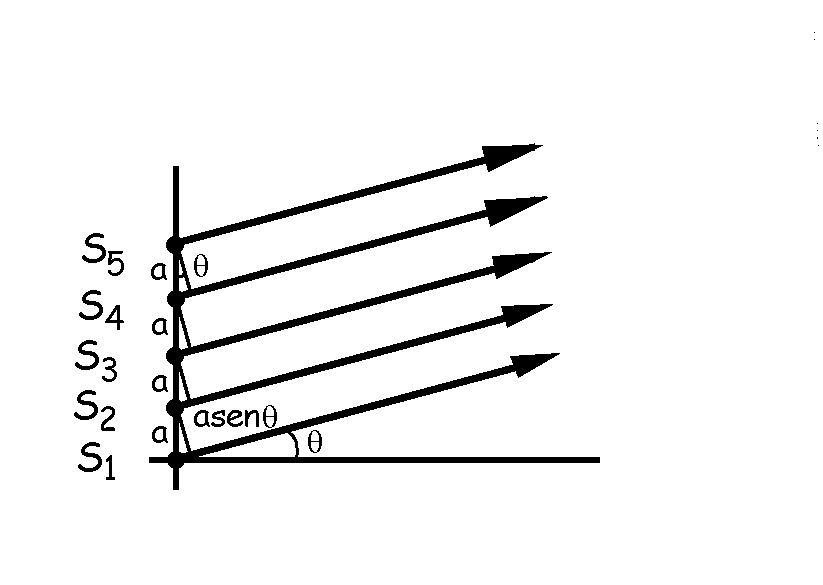 Vamos a ver ahora cuál es la expresión del desfase para N fuentes en el caso de amplitud cero, es decir, destructiva. Denominaremos a a la separación entre las fuentes y supondremos que observamos el diagrama de interferencia sobre un plano o pantalla muy alejada (D>>>a) paralela a la línea de las fuentes, de modo que los rayos que interfieren en un punto P genérico pueden considerarse paralelos. En estas condiciones, entre dos rayos consecutivos habrá una diferencia de camino igual a asenθ, lo que significa un desfase angular δ dado por:
Vamos a ver ahora cuál es la expresión del desfase para N fuentes en el caso de amplitud cero, es decir, destructiva. Denominaremos a a la separación entre las fuentes y supondremos que observamos el diagrama de interferencia sobre un plano o pantalla muy alejada (D>>>a) paralela a la línea de las fuentes, de modo que los rayos que interfieren en un punto P genérico pueden considerarse paralelos. En estas condiciones, entre dos rayos consecutivos habrá una diferencia de camino igual a asenθ, lo que significa un desfase angular δ dado por:
![]()
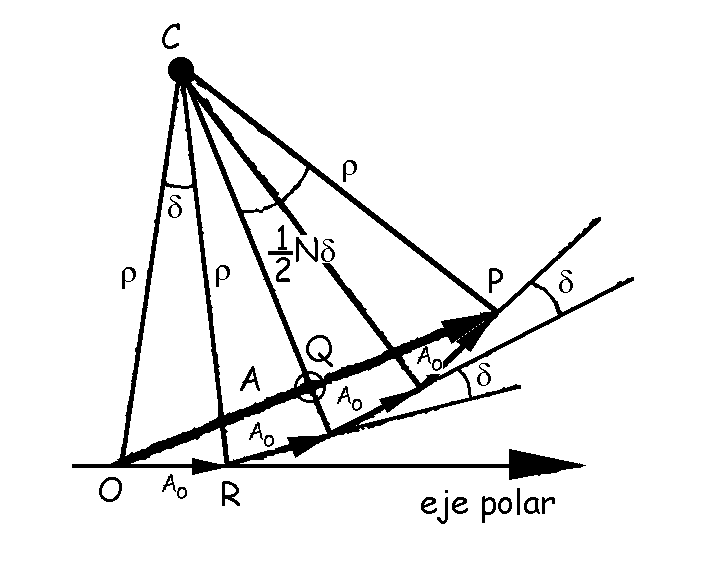 Para obtener la amplitud resultante en la dirección de observación definida por el ángulo θ deberemos sumar fasorialmente, como ya hemos visto, las N contribuciones individuales (denominaremos A0 a la amplitud de cada fuente y A a la amplitud total). Para N fuentes los fasores sucesivos constituyen los lados de un polígono regular incompleto. Un polígono como este puede considerarse inscrito en una circunferencia de radio ρ y centro C, de modo que el ángulo subtendido en C por cada fasor individual es igual a δ y el subtendido por el fasor resultante A es igual a Nδ. Podemos ver que en los triángulos COP y COR se verifica que:
Para obtener la amplitud resultante en la dirección de observación definida por el ángulo θ deberemos sumar fasorialmente, como ya hemos visto, las N contribuciones individuales (denominaremos A0 a la amplitud de cada fuente y A a la amplitud total). Para N fuentes los fasores sucesivos constituyen los lados de un polígono regular incompleto. Un polígono como este puede considerarse inscrito en una circunferencia de radio ρ y centro C, de modo que el ángulo subtendido en C por cada fasor individual es igual a δ y el subtendido por el fasor resultante A es igual a Nδ. Podemos ver que en los triángulos COP y COR se verifica que:
![]()
![]()
por lo que, dividiendo miembro a miembro las expresiones anteriores:
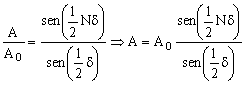
Observando esa expresión podemos ver que la amplitud será nula cuando:
![]()
donde m toma valores desde 1 hasta N-1, N+1 a 2N-1, etc. Se excluyen los valores de m=0, N, 2N, … ya que para ellos la expresión da lugar a la condición de máximo.