a) S=f’
b) Objeto en la lente
c) Si el objeto y la imagen están a la izquierda de la lente ⇒ Objeto a la izquierda de la lente
Si el objeto y la imagen están a la derecha de la lente ⇒ Objeto virtual a distancia 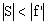
d) S=2f’
e) Objeto virtual a distancia 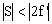
a) Denominaremos f’ al valor absoluto de la focal de la lente. Tendremos que tener en cuenta que como es divergente la focal será negativa. Aplicamos entonces la ecuación de las lentes delgadas, sabiendo que la imagen debe estar en el infinito:
![]()
S=f’
Como la distancia es positiva el objeto estará a la derecha de la lente (objeto virtual) y a una distancia igual a la distancia focal.
b) Tendremos la ecuación de las lentes:
![]()
En esta ecuación, S y S’ toman el mismo valor cuando ambos son nulos. Por tanto ambos deben situarse en el origen, es decir, en la lente, de modo que las distancia entre ellos es nulo.
OBJETO EN LA LENTE
c) Si la imagen es derecha el aumento lateral debe ser positivo. Este aumento es:
![]()
Para que β sea positivo tanto S como S’ deberán tener el mismo signo, es decir, objeto e imagen tienen que estar al mismo lado de la lente. Supongamos en primer lugar que ambos están a la izquierda de la lente, es decir, que ambos son negativos:
![]()
En esta ecuación tanto f’ como S son negativos, y además S’ también debe ser negativo. En el numerador f’S será un número positivo (producto de dos números negativos) luego para que S’ sea negativo el denominador de esa ecuación debe ser negativo. Teniendo en cuenta que tenemos la suma de dos números negativos es obvio que se cumplirá la condición para todo valor de S. Entonces la imagen será derecha siempre que el objeto esté a la izquierda de la lente y a cualquier distancia de ella.
OBJETO A LA IZQUIERDA DE LA LENTE
Supongamos ahora que tanto el objeto como la imagen estén a la derecha de la lente, es decir, S y S’ son positivos. Tendremos como antes la ecuación:
![]()
En esta ecuación el numerador es negativo, puesto que f’ es negativo y S positivo. Por tanto, para que S’ sea positivo el denominador también tendrá que ser negativo. Ahora tenemos la suma de un número positivo (S) y uno negativo (f’). Por tanto esta suma será negativa siempre que f’ sea mayor que S. La imagen será derecha si el objeto es virtual (está a la derecha de la lente) y está a una distancia menor que la distancia focal:
OBJETO VIRTUAL A DISTANCIA |S|<|f’|
d) Si la imagen tiene el mismo tamaño que el objeto el aumento lateral debe ser igual a la unidad (positivo o negativo, ya que no nos dicen que tenga que estar derecho o invertido). Supongamos que β vale la unidad. En este caso:
![]()
Las distancias objeto e imagen son iguales y además tienen el mismo signo. Supongamos que ambas son negativas. Entonces:
![]()
Vemos que no puede verificarse la ecuación de las lentes. Si ambas son positivas:
![]()
Tampoco se verificaría la ecuación de las lentes. Entonces no puede ocurrir que la imagen tenga el mismo tamaño que el objeto y que además esté derecha. Veamos que ocurre si la imagen es invertida respecto del objeto pero tiene su mismo tamaño. En este caso el aumento lateral valdrá -1:
![]()
Las distancias objeto e imagen son iguales en valor absoluto pero tienen distinto signo. Supongamos que S es negativa y S’ positiva. Entonces, aplicando la ecuación de las lentes:
![]()
Vemos que esto tampoco es posible, ya que tenemos un número positivo en el primer miembro y uno negativo en el segundo, luego no pueden ser iguales. Por último, si suponemos que S es positivo y S’ negativo tendremos:
![]()
Ahora sí podría verificarse, si el objeto está a la derecha de la lente (objeto virtual) y a una distancia doble de su focal:
S=2f’
e) Vamos a ver qué tiene que ocurrir para que la imagen esté invertida y aumentada. El aumento lateral deberá ser negativo (S y S’ tienen distinto signo) y además mayor que la unidad (en módulo, S’ será mayor que S). Planteamos pues dos posibilidades. En primer lugar supongamos que S es negativo y S’ positivo. Entonces:
![]()
Esta ecuación no puede verificarse, ya que tenemos que la suma de dos números positivos da uno negativo, lo cual es imposible. Por tanto para un objeto real la imagen no puede estar aumentada e invertida a la vez.
Supongamos ahora que el objeto es virtual, es decir, que S es positivo y S’ negativo. Nos quedará:
![]()
Esta ecuación se verificará siempre, ya que la suma de dos números negativos es un número negativo. Tenemos pues que si el objeto es virtual la imagen está siempre invertida. Si además operamos:
![]()
Para que además la imagen esté aumentada debe cumplirse que S’>S, lo que implica que:
S-f'<f’ ⇒ S<2f’
El objeto debe ser virtual y estar a una distancia inferior al doble de la focal.
OBJETO VIRTUAL A DISTANCIA |S|<|2f’|