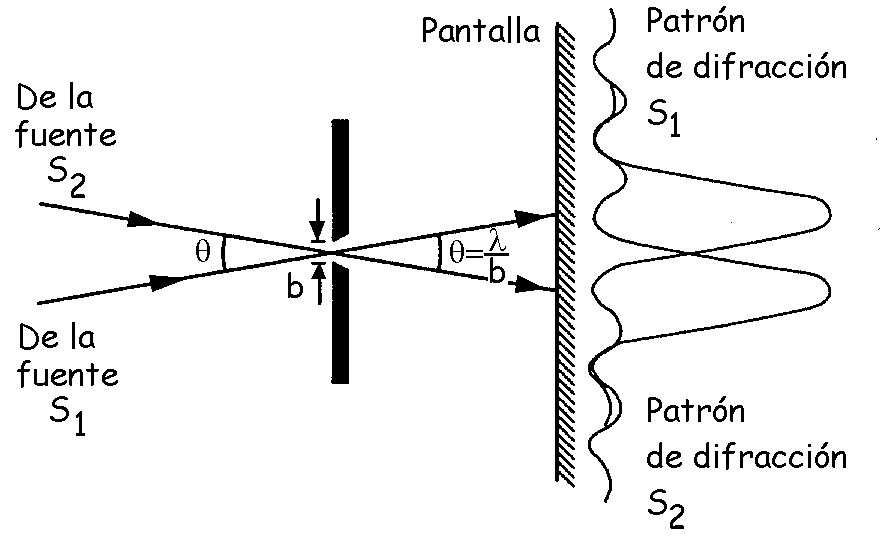
El poder resolvente de una ranura, según la definición de Lord Rayleigh, es el mínimo ángulo subtendido por dos ondas incidentes que provienen de dos fuentes puntuales distantes, cuyos respectivos patrones de difracción se pueden separar. Cuando las ondas que provienen de dos fuentes distantes, S1 y S2, pasan por la misma ranura en dos direcciones formando un ángulo q
(ver figura), los respectivos patrones de difracción se superponen, pero aparecen como distintos cuando el máximo central de uno cae en el primer cero, a cualquier lado del máximo central del otro, como se indica en la parte de la derecha de la figura. Para que esto ocurra, si llamamos b a la anchura de la rendija y λ a la longitud de onda, el ángulo θ debe ser:
que da el poder separador de la ranura según la definición de Rayleigh.
Suponiendo que S1 y S2 son dos puntos de un objeto lejano, la ecuación anterior da la mínima separación angular entre ellos a la que se les puede observar como puntos diferentes cuando el objeto se ve a través de la ranura. Si la luz que pasa por la ranura forma una imagen en una pantalla y ésta se observa, por ejemplo, con un microscopio, sin importar qué aumento tenga, no será posible observar más detalles en la imagen que lo permitido por el poder resolvente de la ranura.